
Канонический анализ. Каноническая корреляция позволяет исследовать зависимость между двумя наборами переменных (и применяется для проверки гипотез или как метод разведочного анализа). Например, исследователь в сфере образования может оценить зависимость между навыками по трем учебным дисциплинам и оценками по пяти школьным предметам. Социолог может исследовать зависимость между прогнозами социальных изменений, печатаемыми в двух газетах, и реальными изменениями, оцененными с помощью четырех различных статистических признаков. Исследователь-медик может изучить зависимость между различными неблагоприятными факторами и появлением определенной группы симптомов. Во всех этих случаях нас интересуют зависимости между двумя группами переменных. Для анализа таких зависимостей и предназначен метод Канонической корреляции.
Дополнительную информацию см. в разделе Канонический анализ.
Карта линий уровня. Карта линий уровня представляет собой проекцию 3М поверхности на 2М плоскость.

В случае, когда требуется быстро представить себе общую трехмерную картину данных, это средство, возможно, будет менее эффективно, чем график поверхности,
однако главное преимущество карт линий уровня
состоит в том, что с их помощью можно детально
исследовать форму поверхности (карты линий
уровня изображаются в виде семейства линий,
получающихся в результате сечения поверхности
горизонтальными плоскостями).
Категоризация, группировка, разбиение на подмножества. Одним из наиболее важных, общих, а также мощных аналитических методов заключается в разделении (разбиении) данных на несколько подмножеств и последующее сравнение структуры данных в полученных подмножествах. У этого общего метода имеется много различных названий (в том числе: разбиение, группировка, категоризация, расщепление, разветвление и условный анализ), и он используется как для разведочного анализа данных, так и для проверки гипотез. Пример: величина (положительного) коэффициента корреляции между возрастом и риском сердечного приступа может различаться у мужчин и женщин (может быть выше у мужчин). Существенное снижение уровня холестерина в крови при приеме определенного лекарства может присутствовать только у женщин в возрасте от тридцати до сорока лет, имеющих низкое кровяное давление. Индексы устойчивости процесса и его гистограммы устойчивости могут различаться во время работы разных операторов. Угловые коэффициенты регрессионных кривых могут быть различными в разных экспериментальных группах.
Существует много методов для учета результатов
группировки, позволяющих обнаружить и
количественно сравнить разницу между группами
(например, дисперсионный
анализ). Тем не менее, графические методы (такие
как категоризованные
графики) представляют уникальные возможности,
преимущества которых не могут быть восполнены
никакими вычислительными методами: они
позволяют обнаружить некоторые структурные
свойства, которые трудно выразить численно
(например, сложные взаимодействия, исключения,
аномалии) и предоставляют уникальные,
многомерные, глобальные аналитические
перспективы для анализа и обработки данных (т.н. добычи данных).
Категоризованная 3М диаграмма отклонений. На графике этого типа точки данных (координаты X, Y и Z) представляются в 3М пространстве в виде "отклонений" от заданного уровня основания по оси Z . Для каждого уровня группирующей переменной (или заданного пользователем подмножества данных) строится один график, и все эти графики изображаются в одном графическом окне, позволяя сравнивать подмножества данных (категории).
Подробное описание Категоризованных
графиков см. в разделе Категоризованные графики
главы Графические методы
анализа данных.
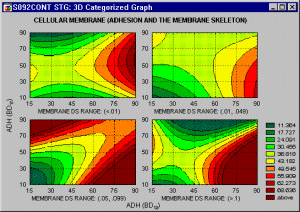
Категоризованная 3М диаграмма рассеяния. С помощью графиков этого типа можно визуально представить зависимость между тремя переменными (соответствующими координатам X, Y и одной или нескольким [вертикальным] координатам Z каждой точки в 3М пространстве), категоризованными посредством группирующей переменной (или заданным пользователем методом категоризации). Для каждого уровня группирующей переменной (или заданного пользователем подмножества данных) строится один график, и все эти графики изображаются в одном графическом окне, позволяя сравнивать подмножества данных (категории) - см. Рис. 1:

Подробное описание Категоризованных
графиков см. в разделе Категоризованные графики
главы Графические методы
анализа данных. См. также Сокращение объема данных.
Категоризованный 3М пространственный график. Этот график является особым способом представления данных 3М диаграммы рассеяния при помощи плоскости XY, расположенной на выбранном пользователем уровне вертикальной оси Z (которая проходит через центр плоскости). Уровень плоскости XY можно менять таким образом, чтобы разделить пространство XYZ на имеющие особый смысл части (например, с разными структурами зависимости между тремя переменными) - см. выше Рис. 2.
Подробное описание Категоризованных
графиков см. в разделе Категоризованные графики
главы Графические методы
анализа данных.
Категоризованная 3М спектральная диаграмма. Этот тип графиков представляет собой несколько спектральных диаграмм (для подмножеств данных, заданных выбранным методом категоризации), изображенных в одном графическом окне, что позволяет сравнивать подмножества данных. Значения переменных X и Z интерпретируются как координаты каждой точки по осям X и Z соответственно; значения переменной Y объединены в группы, соответствующие последовательно расположенным через равные промежутки спектральным плоскостям - см. выше Рис. 3.
Подробное описание Категоризованных
графиков см. в разделе Категоризованные графики
главы Графические методы
анализа данных.
Категоризованные
графики (графики на решетке). Этот тип
графиков дает возможность категоризовать 2М, 3М
или nМ графики с помощью задания категорий
выбранной переменной. Для каждого уровня
группирующей переменной (или заданного
пользователем подмножества данных) строится
один график, и все эти графики изображаются в
одном графическом окне, позволяя сравнивать
различные подмножества (категории). Более
подробное описание категоризованных графиков содержится
в разделе Статистические
категоризованные графики главы Графические методы анализа
данных; см. также Разведочный
анализ и "добыча" данных.
Категоризованные
графики вероятность-вероятность. На этом
статистическом графике подгонку теоретического
распределения к наблюдаемым данным можно
зрительно оценить, исследуя каждый график вероятность-вероятность
(также называемый вероятностным графиком,
см. Статистические графики
вероятность-вероятность) для соответствующего
уровня группирующей
переменной (или заданного пользователем
подмножества данных). Графики вероятность-вероятность
(или В-В) показывают связь функций
наблюдаемого и теоретического кумулятивных
распределений. Как и для категоризованного
графика квантиль-квантиль, значения
переменной сначала упорядочиваются по
возрастанию. Наблюдению с номером i соответствует
значение i/n на одной оси (т.е. функция
наблюдаемого кумулятивного распределения) и
значение F(x(i)) на другой оси, где F(x(i)) есть
значение функции теоретического кумулятивного
распределения для соответствующего наблюдения x(i).
Если теоретическое распределение хорошо
приближает наблюдаемое распределение, то все
точки графика должны попасть на диагональную
линию. Для каждого уровня группирующей
переменной (или заданного пользователем
подмножества данных) строится один график, и все
эти графики изображаются в одном графическом
окне, давая возможность сравнивать подмножества
данных (категории).
Категоризованные графики квантиль-квантиль. На этом статистическом графике подгонку теоретического распределения к наблюдаемым данным можно зрительно оценить, исследуя каждый график квантиль-квантиль (или К-К) (также называемый графиком квантилей, см. Статистические графики квантиль-квантиль) для соответствующего уровня группирующей переменной (или заданного пользователем подмножества данных).
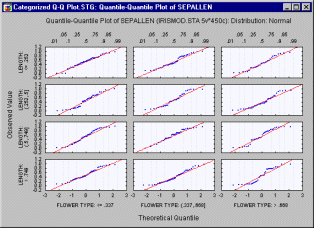
На этом графике показана связь между
наблюдаемыми значениями переменных и
теоретическими квантилями. Если наблюдаемые
значения попадают на прямую линию, то
теоретическое распределение хорошо подходит к
наблюдаемым данным. Для каждого уровня группирующей переменной
(или заданного пользователем подмножества
данных) строится один график, и все эти графики
изображаются в одном графическом окне, давая
возможность сравнивать подмножества данных
(категории). (Описание процедуры построения
графика К-К см. в параграфе Графики
квантиль-квантиль.)
Категоризованные нормальные вероятностные графики. Этот вероятностный график строится следующим образом. Сначала значения внутри каждой категории упорядочиваются по рангу. По этим рангам рассчитываются значения z (т.е. стандартизованные значения нормального распределения) в предположении, что данные имеют нормальное распределение (см. Замечания о методах вычислений). Эти значения z откладываются по оси Y графика. Если наблюдаемые значения (откладываемые по оси X) распределены нормально, то все значения на графике должны попасть на прямую линию. Если значения не являются нормально распределенными, они будут отклоняться от линии. На этом графике можно легко обнаружить выбросы. Если наблюдается очевидное несовпадение, и данные располагаются относительно линии определенным образом (например, в виде буквы S ), то перед применением статистических методов, для которых существенное значение имеет нормальность распределения, необходимо каким-то образом преобразовать переменные (например, логарифмическое преобразование часто используется для того, чтобы "втянуть" конец распределения).
Подробное описание Категоризованных
графиков см. в разделе Категоризованные графики
главы Графические методы
анализа данных.
Категоризованные нормальные вероятностные графики с исключенным трендом. Этот категоризованный график строится тем же способом, что и стандартный нормальный вероятностный график для категоризованных значений, с тем отличием, что перед построением графика удаляется линейный тренд. При этом часто получается более "развернутая" картина, позволяющая пользователю легче обнаружить закономерности отклонений.
Подробное описание Категоризованных
графиков см. в разделе Категоризованные графики
главы Графические методы
анализа данных.
Категоризованные полунормальные вероятностные графики. Категоризованный полунормальный вероятностный график строится тем же способом, что и стандартный нормальный вероятностный график, с тем отличием, что рассматривается только положительная часть нормальной кривой. Таким образом, по оси Y будут откладываться только положительные нормальные значения. Этот тип графиков часто используется для остатков (например, в модели множественной регрессии) в случаях, когда знаки остатков несущественны, т.е. когда нас интересует распределение абсолютных значений остатков, вне зависимости от из знака.
Подробное описание Категоризованных
графиков см. в разделе Категоризованные графики
главы Графические методы
анализа данных.
Категоризованный 3М график поверхности. На этом графике строятся поверхности (полученные сглаживанием или заданные пользовательским математическим выражением) по категоризованным данным (переменным, соответствующим наборам координат XYZ), т.е. подмножествам данных, заданных выбранным методом категоризации, причем все они изображаются в одном графическом окне, что дает возможность сравнивать эти подмножества (категории).

Подробное описание Категоризованных
графиков см. в разделе Категоризованные графики
главы Графические методы
анализа данных.
Качество (в анализе соответствий). Термин качество в анализе соответствий включает информацию о качестве представления соответствующей точки-строки в координатной системе выбранной размерности. Качество точки определяется как отношение квадрата расстояния - от данной точки до начала координат в пространстве выбранной размерности - к квадрату расстояния до начала координат, определенному в пространстве максимальной размерности (в качестве метрики в анализе соответствий как правило выбирается метрика хи-квадрат). По аналогии с факторным анализом, качество точки похоже по интерпретации на показатель общности переменной в факторном анализе.
Низкое качество означает, что выбранное
измерение недостаточно хорошо представляет
соответствующую строку (столбец).
Квадратичная
функция ошибок. Функция ошибок, равная
сумме (взятой по всем наблюдениям) квадратов
разностей целевых и фактических значений (см.
также функция потерь).
Квадратичное
сглаживание. К точкам 3М диаграммы
рассеяния подгоняется полином второй степени.
Квази-ньютоновский
метод. Процедура нелинейного
оценивания, вычисляющая на каждом шаге
значения функции в различных точках для
оценивания первой и второй производной, и
использующая эти данные для определения
направления изменения параметров и минимизации функции потерь.
Квантили. Квантиль (термин был впервые использован Кендаллом в 1940 г.) распределения значений - это такое число xp , что значения p-й части совокупности меньше или равны xp . Например, квантиль 0.25 (также называемая 25-й процентилью или нижней квартилью) для некоторой переменной - это такое значение (xp), что 25% (p) значений переменной не превосходят этого значения.
Аналогично, квантиль 0.75 (также называемая 75-й процентилью или верхней квартилью) - это такое значение, ниже которого попадают 75% значений переменной.
См. также Графики
квантиль-квантиль.
Квартили. Нижняя и верхняя квартили (термин был впервые использован Галтоном, 1882; также их называют квантилями 0.25 и 0.75) равны соответственно 25-й и 75-й процентилям распределения. 25-я процентиль переменной - это такое значение, ниже которого попадают 25% значений переменной.
Аналогично, 75-я процентиль - это такое значение,
ниже которого попадают 75% значений переменной.
Квартильный размах. Квартильный размах переменных (термин был впервые использован Галтоном в 1882 г.) равен разности значений 75-й процентили и 25-й процентили. Таким образом, это тот диапазон вокруг медианы, который содержит 50% наблюдений.
Для получения более подробной информации см.
главу Непараметрическая
статистика.
Классификация. Отнесение
наблюдения к одному из нескольких, заранее
известных классов (представленных значениями номинальной выходной
переменной).
Кластерный
анализ. Термин кластерный анализ (впервые
ввел Tryon, 1939) в действительности включает в себя
набор различных алгоритмов
классификации. Общий вопрос, задаваемый
исследователями во многих областях, состоит в
том, как организовать наблюдаемые данные в
наглядные структуры, т.е. развернуть таксономии
(обычно в разведочном
анализе) или определить кластеры схожих
объектов. Например, биологи ставят цель разбить
животных на различные виды, чтобы содержательно
описать различия между ними. В соответствии с
современной системой, принятой в биологии,
человек принадлежит к приматам, млекопитающим,
амниотам, позвоночным и животным. Заметьте, что в
этой классификации, чем выше уровень агрегации,
тем меньше сходства между членами в
соответствующем классе. Человек имеет больше
сходства с другими приматами (т.е. с обезьянами),
чем с "отдаленными" членами семейства
млекопитающих (например, собаками) и т.д.
Информацию о методах кластерного анализа см.
в разделах Объединение
(древовидная кластеризация), Двувходовое объединение и Метод K средних.
За дополнительной информацией обратитесь к
главе Кластерный анализ ; см.
также Деревья классификации.
Ковариаты,
зависящие от времени. Зависящие от времени
ковариаты используются, когда эффект от
ковариаты на времена жизни зависит от времени
(т.е. условная интенсивность в каждый момент
времени является функцией ковариаты и времени).
Кодирование
N-в-одну. Для номинальных
переменных с числом значений, большим двух, -
способ представления переменной с помощью
одного элемента сети через его различные
выходные значения (используется в вариантах: минимакс, явное и нет). См. также Нейронные сети.
Кодирование
один-из-N (для нейронных сетей). Представление
номинальной переменной
с помощью набора входных или выходных элементов -
по одному на каждое возможное номинальное
значение. Во время обучения сети один из этих
элементов бывает активен, а остальные -
неактивны. См. Нейронные сети
Коды (значения
группирующих переменных). Коды
представляют собой значения группирующей переменной
(например, 1, 2, 3, ... или Муж, Жен), которые
определяют уровни группирующей переменной для
анализа. Коды могут быть как целочисленными, так
и текстовыми значениями.
Комплексные числа. Комплексные числа - это множество чисел, которое включает все действительные и мнимые числа. Комплексное число представляется выражением вида a + ib, где a и b - действительные числа, i - мнимая единица, т.е. такое число, что i**2=-1.
См. также Кросс-спектральный
анализ в главе Временные
ряды.
Компоненты дисперсии (в смешанной модели дисперсионного анализа) Термин компоненты дисперсии используется в контексте дисперсионного анализа и планирования эксперимента, включающего случайные эффекты, для обозначения оценки (доли) дисперсии, которая связана с этими эффектами. Например, если нас интересует влияние образовательного уровня школы на теоретическую подготовленность учеников, мы можем создать выборку из различных школ для оценивания доли дисперсии теоретических подготовленности учеников (компоненты дисперсии), связанной с различиями между школами.
Для получения дополнительной информации см.
разделы Дисперсионный анализ
и Компоненты дисперсии и
смешанная модель ANOVA/ANCOVA.
Контроль качества. Для всех производственных процессов возникает необходимость установить пределы характеристик изделия, в рамках которых произведенная продукция удовлетворяет целевому назначению. Существует два "врага" качества продукции: (1) уклонения от значений плановых спецификаций изделия и (2) слишком высокая изменчивость (разброс) реальных характеристик изделий относительно значений плановых спецификаций. На более ранних стадиях отладки производственного процесса для оптимизации этих двух показателей качества производства часто используются методы планирования эксперимента (см. Планирование эксперимента). Методы, описанные в главе Контроль качества, предназначены для построения процедур контроля качества продукции непосредственно в процессе ее производства
Общий подход к текущему контролю качества прост. В процессе производства проводится отбор выборок изделий заданного объема. После этого на специально разлинованной бумаге строятся диаграммы изменчивости выборочных значений плановых спецификаций в этих выборках и рассматривается степень их близости к плановым значениям. Если диаграммы обнаруживают наличие тренда выборочных значений или выборочные значения оказываются вне заданных пределов, то считается, что процесс вышел из-под контроля, и предпринимаются необходимые действия для того, чтобы найти причину его разладки. Иногда такие специально разлинованные листы бумаги называют контрольными картами Шуэрта (в честь W. A. Shewhart, который общепризнанно считается первым, применившим на практике описываемые здесь методы анализа; см. Shewhart, 1931).
Для получения дополнительной информации см.
главу Карты контроля качества.
Контрольные карты Шуэрта. Стандартное графическое средство, широко используемое в статистическом контроле качества. Общий подход к построению контрольных карт можно описать следующим образом: извлекаются выборки определенного размера из произведенной на предприятии продукции и измеряются характеристики качества. Затем строятся кривые, соответствующие измеренным характеристикам и оценивается их близость к заданным плановым спецификациям. Если на полученных кривых отчетливо присутствует тренд или выборочные характеристики попадают вне заданные границы допуска, то процесс объявляется вышедшим из-под контроля и оператор должен предпринять меры, чтобы обнаружить причины, вызвавшие нарушение качества. Названы в честь W. A. Shewhart, который общепризнанно считается первым, применившим на практике описываемые здесь методы анализа; см. Shewhart, 1931.
Дополнительную информацию см. в разделах Карты контроля качества; Объясняемые причины и
действия.
Корректировка X-11. Вывод: A 1. Исходный ряд. Эта таблица процедуры X-11 содержит ряд в его исходном виде, до каких-либо его корректировок пользователем или поправок на число рабочих дней. Для рядов квартальной периодичности нельзя вводить априорные поправки, и исходный ряд будет выдаваться как таблица B 1.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11.
Вывод: A 2. Априорные месячные поправки. Корректировка
X-11 Вывод: A 2. Априорные месячные поправки
В случае ряда ежемесячных значений пользователь
может задать другой ряд, содержащий априорные
ежемесячные поправочные коэффициенты, для того
чтобы, например, учесть непредусмотренный
праздничный день и т.п. Заданные таким образом
поправочные значения будут вычитаться из
исходного ряда в случае аддитивной модели, а в
случае мультипликативной сезонной
корректировки значения исходного ряда будут
поделены на эти поправки (таким образом, в
последнем случае ряд поправок не должен
содержать нулевых значений).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: A 3. Исходный ряд, скорректированный с помощью априорных месячных поправок. Поправки, заданные в A 2, вычитаются из значений исходного ряда (аддитивная корректировка) или значения исходного ряда делятся на эти коэффициенты (мультипликативная корректировка). Данная таблица содержит ряд, получающийся в результате такой корректировки.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: A 4. Априорные поправки на рабочие дни. Эта таблица процедуры X-11 доступна (применима) только в случае, если были заданы априорные поправки на число рабочих дней (для мультипликативных моделей). Пользователь имеет возможность задать вес для каждого дня недели; эти веса затем автоматически пропорционально изменяются, так чтобы их сумма была равна 7. После этого значения ряда (A 1 или A 3) делятся на месячные календарные поправки, которые вычисляются с учетом количества различных дней недели в данном месяце. По умолчанию в календарные эффекты включаются поправки на разное число дней в месяце; кроме того, различия в числе дней в месяце могут быть включены в календарные поправки (в этом случае считается, что все месяцы имеют одинаковую продолжительность, равную 30.4375 дней).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 1. Ряд после априорной корректировки либо исходный ряд. Эта таблица содержит исходный ряд или априорно скорректированный ряд, смотря по тому, были или не были заданы априорные ежемесячные поправки и/или поправки на число рабочих дней (в квартальном варианте метода X-11, таблица B 1 всегда содержит исходный ряд).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 2. Тренд-цикл. Здесь вычисляется предварительная оценка тренд-циклической компоненты как центрированное 12-периодное скользящее среднее ряда B 1.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 3. Немодифицированные S-I разности или отношения. Предварительная оценка суммы нерегулярной и сезонной компонент получается вычитанием ряда B 2 из ряда B 1 (аддитивная модель) или делением B 1 на B 2 (мультипликативная модель).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 4. Значения для замены выбросов S-I разностей (отношений). Сначала вычисляется предварительная оценка сезонной компоненты с помощью взвешенных 5-точечных скользящих средних, примененных к данным из B 3 раздельно по каждому месяцу года. Затем вычисляется центрированное 12-точечное скользящее среднее для предварительных поправок всего ряда в целом, и полученные значения корректируются таким образом, чтобы их сумма за каждый год равнялась нулю (аддитивная модель) или 12.0 (мультипликативная модель). Затем получается начальная оценка нерегулярной компоненты как результат вычитания из S-I разности (аддитивная модель) или деления S-I отношения на начальную оценку сезонной компоненты. Для полученной начальной оценки нерегулярной компоненты вычисляется 5-летнее скользящее стандартное отклонение (s - сигма), и значения в серединный год, выходящие за границы 2.5*s, отбрасываются. Затем вновь вычисляется 5-летнее скользящее s и процесс повторяется; при этом значениям-выбросам, лежащим вне интервала 2.5*s, присваивается нулевой вес, значениям, лежащим внутри интервала 1.5*s, присваивается полный (единичный) вес, а для значений, лежащих между 1.5*s и 2.5*s, выбираются веса, линейно спадающие от 0 к 1. Затем каждое значение, получившее неполный вес, пересчитывается как среднее из него самого, умноженного на свой вес, и двух ближайших соседних значений (одного слева и одного справа) за этот же месяц, имеющих полный вес. Таблица B 4 содержит подставленные (пересчитанные) значения и скользящие 5-летние s.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 5. Сезонная составляющая. Значения-выбросы в ряде B 3 заменяются соответствующими значениями из B 4. Из этого ряда получается предварительная сезонная составляющая взятием 5-точечного скользящего среднего отдельно для значений, соответствующих каждому месяцу; затем берется 12-точечное скользящее среднее для всего ряда, и полученные значения для каждого года корректируются на нулевую сумму (аддитивная модель) или на сумму 12.0 (мультипликативная модель).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 6. Сезонная корректировка ряда. Предварительный вариант сезонно скорректированного ряда получается вычитанием из B 1 сезонной составляющей B 5 (аддитивная модель) или делением B 1 на эту составляющую (мультипликативная модель).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 7. Тренд-цикл. Ряд с поправкой на сезонность (B 6) сглаживается методом регулируемого скользящего среднего (подробности см. в Shiskin, Young, and Musgrave, 1967). По желанию пользователя из сглаженного ряда можно удалить выбросы с помощью процедуры, аналогичной описанной в B 4. В общем случае применяется кривая Хендерсона скользящего среднего, дающая взвешенное скользящее среднее с весами, определяемыми кривой колоколообразной формы (см., например, Makridakis and Wheelwright, 1978, или Shiskin, Young, and Musgrave, 1967). Правильный выбор ширины окна скользящего среднего имеет важное значение для сезонной декомпозиции (т.е. для вычисления тренд-циклической компоненты). Основная идея состоит в том, чтобы выбирать более длинное скользящее среднее, когда в данных присутствуют случайные колебания, большие по величине по сравнению с тренд-циклической компонентой, и более короткое скользящее среднее, когда случайные колебания относительно малы. По умолчанию программа сама выберет параметры скользящего среднего. Более конкретно, вначале вычисляется предварительное 13-точечное взвешенное по Хендерсону скользящее среднее сезонно скорректированного ряда (без продолжения его до границ ряда). Затем вычисляется предварительная оценка нерегулярной компоненты путем вычитания этого ряда из (аддитивная модель) или деления на него (мультипликативная модель) сезонно скорректированного ряда. После этого вычисляется средняя разность (или относительное изменение) от месяца к месяцу без учета знака для оцененных нерегулярной и тренд-циклической компонент. Отношение средних месячных разностей (относительных изменений) для этих двух рядов говорит о степени важности нерегулярных изменений по сравнению с изменениями тренд-циклической компоненты. В зависимости от величины этого отношения берется 9-точечное скользящее среднее Хендерсона (если отношение лежит между 0.0 и 0.99), 13-точечное скользящее среднее Хендерсона (от 1.0 до 3.49) или 23-точечное скользящее среднее Хендерсона (больше 3.5).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 8. Немодифицированные S-I разности (отношения). Эта таблица процедуры X-11 совпадает с таблицей B 3 с той разницей, что она получается из тренд-циклической компоненты, вычисленной в B 7.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 9. Значения для замены выбросов S-I разностей (отношений). Эта таблица процедуры X-11 совпадает с таблицей B 4 с той разницей, что 7-точечное скользящее среднее применяется (для оценки сезонной компоненты) к разностям (отношениям), полученным в B 8.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 10. Сезонная составляющая. После замены значений-выбросов на соответствующие значения из B 9, 7-точечное взвешенное скользящее среднее применяется к S-I разностям (отношениям) в B 8. Полученная оценка сезонной составляющей затем корректируется таким образом, чтобы сумма ее значений за каждый год равнялась нулю (аддитивная модель) или 12.0 (мультипликативная модель).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 11. Сезонная корректировка ряда. Эта таблица совпадает с B 6 с той разницей, что здесь используется сезонная составляющая B 10.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 13. Нерегулярная составляющая ряда. Оценка тренд-циклической компоненты B 7 вычитается из сезонно скорректированного ряда B 11 (аддитивная модель), или же значения ряда B 11 делятся на значения ряда B 7. Полученный в результате ряд представляет собой улучшенную оценку нерегулярной компоненты.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 14. Выбросы нерегулярной составляющей, исключенные из регрессии рабочих дней. Все месяцы в рядe делятся на разные группы в зависимости от того, на какой день недели приходится первый день месяца (при этом 30-дневные, 31-дневные месяцы и феврали обрабатываются раздельно). Затем по двухэтапной процедуре внутри каждого типа месяца находятся выбросы (значения вне интервала 2.5 * s; можно задать различные кратные значения s). Полученные таким образом выбросы подлежат исключению из дальнейшего анализа и собраны в этой таблице.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 15. Предварительная регрессия рабочих дней. После удаления выбросов B 14 из B 13, вычисляются оценки наименьших квадратов для весов семи дней недели.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 16. Поправки на число рабочих дней, полученные из коэффициентов регрессии. По весам регрессии рабочих дней и количеству рабочих дней в месяце вычисляются ежемесячные поправки. Эти поправки представлены в данной таблице и используются затем для корректировки (т.е. вычитаются или служат делителем) ряда нерегулярной составляющей B 13 на число рабочих дней.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 17. Предварительные веса нерегулярной составляющей. Оценки для нерегулярной компоненты (B 13 или скорректированные с помощью B 16, смотря по тому, делалась ли поправка на число рабочих дней) уточняются с помощью вычисления градуированных весов для выбросов, зависящих от их относительных (в терминах 5-летнего скользящего s) расстояния от нуля. Более конкретно, применяется процедура, аналогичная описанной в B 4. Данная таблица (B 17) содержит получающиеся в результате этих действий поправки.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 18. Поправки на число рабочих дней, полученные из комбинированных весов дней недели. Эта таблица содержит окончательные поправки на рабочие дни, вычисленные по оценкам наименьших квадратов для весов дней недели B 15 и/или априорным весам дней недели A 4.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: B 19. Исходный ряд с поправками на рабочие дни и априорную вариацию. Значения B 18 используются для корректировки исходного (или априорно скорректированного) ряда (A 1, A 3 или B 1, в зависимости от того, задавались ли априорные поправки). Конкретно, значения B 18 вычитаются из (аддитивная модель) или служат делителем (мультипликативная модель) значений исходного ряда.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 1. Исходный ряд, модифицированный с помощью предварительных весов, с поправкой на рабочие дни и априорную вариацию. Ряд B 19 (или B 1, если не требуется вносить поправку на рабочие дни) корректируется на выбросы с помощью весов, вычисленных в B 17. В данную таблицу (C 1) помещается полученный в результате этого модифицированный ряд.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 2. Тренд-цикл. Оценка составной тренд-циклической компоненты вычисляется по ряду C 1 с помощью центрированного 12-точечного скользящего среднего.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 4. Модифицированные S-I разности (отношения). Уточненные S-I разности (отношения) получаются вычитанием значений ряда C 2 из (аддитивная модель) или делением на них (мультипликативная модель) модифицированного ряда C 1.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 5. Сезонная составляющая. Те же значения, что в B 5, только используются разности (отношения) C 4.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 6. Сезонная корректировка ряда. Предварительный вариант ряда с сезонной поправкой находится вычитанием C 5 из (или делением на C 5) ряда C 1.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 7. Тренд-цикл. Ряд с поправкой на сезонность (C 6) сглаживается с помощью процедуры регулируемого скользящего среднего (той же, что и в B 7, подробности см. в Shiskin, Young, and Musgrave, 1967) для получения предварительной оценки тренд-циклической компоненты.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 9. Модифицированные S-I разности (отношения). Модифицированные S-I разности (отношения) вычисляются путем вычитания ряда C 7 из ряда C 1, (аддитивная модель) или делением на C 7 (мультипликативная модель) ряда C 1.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 10. Сезонная составляющая. Сезонная составляющая вычисляется аналогично B 10, но на этот раз с использованием S-I разностей (отношений) C 9.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 11. Сезонная корректировка ряда. Уточненный ряд с сезонной поправкой получается вычитанием ряда C 10 из ряда B 1 (аддитивная модель) или делением на C 10 (мультипликативная модель) ряда B 1.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 13. Нерегулярная составляющая. Уточненная оценка нерегулярной (случайной) компоненты получается вычитанием значений ряда C 7 из (аддитивная модель) или делением на них (мультипликативная модель) ряда C 11.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 14. Выбросы нерегулярной составляющей, исключенные из регрессии рабочих дней. Эта таблица аналогична таблице B 14 и содержит выбросы нерегулярной составляющей (как правило, значения, лежащие вне интервала 2.5 * s) после повторного анализа на рабочие дни (с помощью ежемесячных поправок на рабочие дни B 16).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 15. Регрессия рабочих дней - окончательный вариант. Таблица аналогична таблице B 15, только теперь в вычислениях используются значения ряда C 13.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 16. Поправки на число рабочих дней, полученные из коэффициентов регрессии, - окончательный вариант. Эта таблица аналогична таблице B 16 с той разницей, что поправки вычитаются из ряда C 13 (аддитивный случай) или на них делятся (мультипликативный случай) значения ряда C 13.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 17. Окончательные веса нерегулярной компоненты. Эта таблица аналогична таблице B 17, но теперь используются значения C 16 (или C 13, если поправка на число рабочих дней не требуется).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 18. Поправки на число рабочих дней, полученные из комбинированных весов дней недели - окончательный вариант. Эта таблица аналогична таблице B 18, с той разницей, что здесь используются окончательные веса из таблицы C 15.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: C 19. Исходный ряд с поправками на рабочие дни и априорную вариацию. Значения из C 18 используются для корректировки исходного (или априорно скорректированного) ряда (A 3 или B 1). Конкретно, из значений исходного ряда вычитаются значения ряда C 18 (аддитивная модель) или он делится на значения ряда C 18 (мультипликативная модель).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: D 1. Исходный ряд, модифицированный с помощью окончательных весов, с поправкой на рабочие дни и априорную вариацию. Эта таблица аналогична таблице C 1 с той разницей, что при вычислении ее значений используются веса C 17 и скорректированный ряд C 19.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: D 2. Тренд-цикл. В качестве оценки для тренд-циклической компоненты берется 12-точечное скользящее среднее ряда D 1.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: D 4. Модифицированные S-I разности (отношения). Модифицированные S-I разности (отношения) вычисляются вычитанием ряда D 2 из (аддитивная модель) D 1 или делением на D 2 (мультипликативная модель) значений ряда D 1.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: D 5. Сезонная составляющая. Значения в этой таблице вычисляются аналогично B 5, с той разницей, что теперь используются значения из D 4.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: D 6. Сезонная корректировка ряда. Значения в этой таблице получаются вычитанием D 5 из D 1 (аддитивная модель) или делением D 1 на D 5 (мультипликативная модель).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: D 7. Тренд-цикл. Значения в этой таблице вычисляются аналогично B 7 с той разницей, что теперь используются значения из D 6.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: D 8. Немодифицированные S-I разности (отношения) - окончательный вариант. Значения ряда D 7 вычитаются (аддитивная модель) из ряда C 19 или на них делятся (мультипликативная модель) значения ряда C 19 (или B 1, если поправка на число рабочих дней не применяется). Затем ряд подвергается помесячному (или поквартальному) дисперсионному анализу с целью проверить присутствие устойчивой значимой сезонности.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: D 9. Окончательные значения для замены выбросов S-I разностей (отношений). Значения ряда D 7 вычитаются (аддитивная модель) из ряда D 1 или на них делятся (мультипликативная модель) значения ряда D 1. Значения, не совпадающие с соответствующими значениями ряда D 8, фиксируются, затем отображаются на экране. Далее для каждого месяца вычисляются разница год от года (аддитивная модель) или относительное изменение (мультипликативная модель) в оценках для нерегулярной и сезонной компонент, а также их отношение (которое называется MSR). MSR может оказаться полезным для определения доли скользящей сезонности в каждом месяце.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: D 10. Сезонная составляющая - окончательный вариант. Эта таблица вычисляется аналогично B 10, но уже по значениям, содержащимся в D 8 и D 9.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: D 11. Сезонная корректировка ряда - окончательный вариант. Окончательный вариант ряда с сезонной поправкой получается вычитанием D 10 из C 19 (аддитивная модель) или делением C 19 на D 10 (мультипликативная модель).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: D 12. Тренд-циклическая компонента - окончательный вариант. Значения этого ряда получаются вычитанием значений D 10 из D 1 (аддитивная модель) или делением D 1 на D 10 (мультипликативная модель).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: D 13. Нерегулярная составляющая - окончательный вариант. Значения этого ряда получаются вычитанием значений D 12 из D 11 (аддитивная модель) или делением D 11 на D 12 (мультипликативная модель).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: E 1. Модифицированный исходный ряд. Значения в этой таблице получаются заменой выбросов в исходном ряду (которые отличаются от других значений нулевыми весами в C 17) на значения, спрогнозированные по окончательным вариантам тренд-циклической и сезонной компонент, компоненты рабочих дней (если применялась) и априорной корректировки (если применялась).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: E 2. Модифицированный ряд с сезонной поправкой. Значения этого ряда получаются заменой выбросов (значений, имеющих нулевые веса в C 17) в окончательном варианте сезонно скорректированного ряда (D 11) на соответствующие значения окончательного варианта тренд-циклической компоненты D 12.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: E 3. Модифицированная нерегулярная составляющая. Значения в этой таблице получаются заменой соответствующих значений D 13 на нулевые значения (аддитивная модель) или на единицу (мультипликативная модель) в случае, если они были идентифицированы как выбросы (т.е. получили нулевые веса) в C 17.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: E 4. Разности (отношения) годовых сумм. Значения в этой таблице вычисляются как разности (аддитивная модель) или отношения (мультипликативная модель) суммарных значений за год (1) исходного ряда B 1 и окончательного варианта ряда с поправкой на сезонность D 11, и (2) модифицированного исходного ряда E 1 и модифицированного ряда с поправкой на сезонность E 2.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: E 5. Разности (относительные изменения) исходного ряда. Значения в этой таблице вычисляются как разности от месяца к месяцу (квартала к кварталу) - (аддитивная модель) или относительные изменения (мультипликативная модель) ряда B 1.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: E 6. Разности (относительные изменения) окончательного варианта ряда с сезонной поправкой. Эти значения представляют собой разности от месяца к месяцу (квартала к кварталу) - (аддитивная модель) или относительные изменения (мультипликативная модель) ряда D 11.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: F 1. МЦД (КЦД) скользящее среднее. Значения этого ряда получаются применением процедуры невзвешенного скользящего среднего к окончательному варианту ряда с сезонной поправкой (D 11). Ширина окна сглаживания определяется месяцем (кварталом) циклического доминирования, сокращенно МЦД (КЦД). МЦД (или КЦД) вычисляется как средний отрезок времени, на котором изменения случайной составляющей становятся равными изменениям тренд-циклической компоненты.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: F 2. Сводные показатели. Здесь вычисляется несколько таблиц, содержащих сводные показатели:
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: G 1. График. На этом графике будет изображен окончательный вариант ряда с сезонной поправкой и окончательный вариант тренд-циклической компоненты (соответственно D 11 и D 12).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: G 2. График. На этом графике изображаются окончательные S-I разности (аддитивная модель) или отношения (мультипликативная модель), включая выбросы, окончательные S-I разности (отношения) без выбросов и окончательные сезонные поправки (D 8, D 9 и D 10, соответственно), категоризованные по месяцам (только для месячного варианта X-11) или кварталам (для квартального варианта X-11).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: G 3. График. На этом графике представлены те же значения, что и на G 2; только расположенные в хронологическом порядке.
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корректировка X-11. Вывод: G 4. График. На этом графике представлены окончательный вариант нерегулярной компоненты и окончательный вариант модифицированной нерегулярной компоненты (соответственно, D 13 и E 3).
За дополнительной информацией обратитесь к
разделу Сезонная
корректировка X-11 (метод Census II).
Корреляция. Корреляция - это мера связи между двумя переменными. Коэффициент корреляции может изменяться от -1.00 до +1.00. Значение -1.00 означает полностью отрицательную корреляцию, значение +1.00 означает полностью положительную корреляцию. Значение 0.00 означает отсутствие корреляции.
См. также Корреляции, Частные корреляции, Корреляция Пирсона, Ложная корреляция.
Корреляция Пирсона. Наиболее часто используемый коэффициент корреляции Пирсона r (Pearson, 1896) называется также линейной корреляцией (термин корреляция впервые ввел Galton, 1888), т.к. измеряет степень линейных связей между переменными. Можно сказать, что корреляция определяет степень, с которой значения двух переменных пропорциональны друг другу. Важно, что значение коэффициента корреляции не зависит от масштаба измерения. Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения в дюймах и футах или в сантиметрах и килограммах. Пропорциональность означает просто линейную зависимость. Корреляция высокая, если на графике зависимость можно представить прямой линией (с положительным или отрицательным углом наклона). Проведенная прямая называется прямой регрессии или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленная по оси Y) от наблюдаемых точек до прямой является минимальной из всех возможных. Заметим, что использование квадратов расстояний приводит к тому, что на оценки параметров сильно влияют выбросы. Корреляция Пирсона предполагает, что две рассматриваемые переменные измерены, по крайней мере, в интервальной шкале. Коэффициент корреляции Пирсона вычисляется следующим образом:
r12 = [![]() (Yi1 - Y-bar1)*(Yi2 - Y-bar2)]
/ [
(Yi1 - Y-bar1)*(Yi2 - Y-bar2)]
/ [![]() (Yi1 - Y-bar1)2
*
(Yi1 - Y-bar1)2
* ![]() (Yi2 - Y-bar2)2]1/2
(Yi2 - Y-bar2)2]1/2
См. также Корреляции -
Обзор.
Косинус-сглаживание. Так называемый процесс косинус-сглаживания в анализе временных рядов - рекомендуемое преобразование ряда, предшествующее спектральному анализу. Оно обычно приводит к уменьшению рассеяния в периодограмме. Логическое обоснование этого преобразования подробно объясняется в книге Блумфилда (Bloomfield, 1976, стр. 80-94). По существу, (p) доля данных в начале и в конце ряда преобразуется по формуле:
wt = 0.5*{1-cos[![]() *(t - 0.5)/m]} (for t=0 to m-1)
*(t - 0.5)/m]} (for t=0 to m-1)
wt = 0.5*{1-cos[![]() *(N - t +
0.5)/m]} (for t=N-m to N-1)
*(N - t +
0.5)/m]} (for t=N-m to N-1)
где m выбирается так, чтобы
выполнялось 2*m/N = p.
Кохонена обучение. Алгоритм, размещающий центры кластеров радиального слоя посредством последовательной подачи на вход сети обучающих наблюдений и корректировки положения центра выигравшего (ближайшего) радиального элемента и соседних с ним в сторону обучающего наблюдения (Kohonen, 1982; Fausett, 1994; Haykin, 1994; Patterson, 1996).
См. Нейронные сети .
Кохонена сети. Нейронные сети, основанные на воспроизведении топологических свойств человеческого мозга. Известны также как самоорганизующиеся карты характеров (SOFM) (Kohonen, 1982; Fausett, 1994,; Haykin, 1994; Patterson, 1996).
Коэффициент детерминации. Это квадрат корреляции Пирсона между двумя переменными (rІ). Он выражает количество дисперсии, общей между двумя переменными.
См. также работу Hays, 1988.
Коэффициент несогласия. Коэффициент несогласия полезен для описания результатов логистической регрессии (см. работу Neter, Wasserman, and Kutner, 1989) и вычисляется на основании таблицы 2x2, в ячейках которой показано количество наблюдаемых и предсказанных значений для бинарных зависимых переменных:
(f11 * f22)/(f12 * f21)
где fij представляет
соответствующие частоты в таблице 2x2.
Краткие
контрольные карты. Краткая
контрольная карта используется при контроле
качества в кратких производственных сериях
(различных частях одного процесса). В составе
данной карты на одном графике выводятся
преобразованные значения наблюдаемых значений
переменных или альтернативных признаков -
характеристик частей процесса, каждая из которых
образует отдельную производственную серию.
Применяемые в данном типе карт преобразования
заключаются в таком изменении масштаба
контролируемых переменных, при котором
амплитуды данных переменных в различных
производственных сериях (различных частях
процесса) будут сравнимыми. Для преобразованных
таким образом значений переменных вычисляются
контрольные пределы, которые могут быть
применены в дальнейшем для выявления
наступившей разладки процесса, для текущего
контроля качества выпускаемой продукции и
разработки методов постоянного улучшения
качества.
Кривые Джонсона. Джонсон (1949) описал систему плотностей, получающихся преобразованием стандартной нормальной плотности (см. Hahn and Shapiro, 1967). Применяя эти преобразования к стандартной нормальной переменной (т.е. переменной со средним 0 и стандартным отклонением 1) можно аппроксимировать различные распределения, отличные от нормальных, включая распределения, сосредоточенные на полуосях или компактах (например, имеющие U-образную форму). Преимущество этого подхода в том, что если однажды кривая Джонсона была подогнана к данным, то затем можно использовать стандартное нормальное распределение для вычисления нужных процентных точек. Методы подгонки кривых Джонсона, а также приближенные формулы для первых четырех моментов даны Hahn and Shapiro, 1967, стр. 199-220; Hill, Hill, and Holder, 1976. Сравнение распределений Джонсона и Пирсона дано в Технических замечаниях модуля Анализ процессов.
См. также кривые Пирсона.
Кривые операционных характеристик для карт контроля качества. Часто используемым дополнительным графиком для стандартных карт контроля качества является так называемая кривая операционных характеристик (или ОХ-кривая). Одним из вопросов, возникающим при использовании стандартной карты по переменной или атрибуту, является вопрос о том, насколько чувствительна текущая процедура контроля качества. Или, говоря более точно, какова вероятность того, что мы не заметим выхода выборки (например выборочного среднего на X-карте) за контрольные границы (т.е. посчитаем состояние производственного процесса допустимым), когда на самом то деле процесс отклонился на определенную величину? Эту вероятность обычно называют вероятностью b (бета)-ошибки, т.е. это вероятность ошибочного заключения о допустимости процесса (среднего, отношения средних, среднего уровня бракованных изделий, и т.п.), в то время как процесс выходит за контрольные границы.
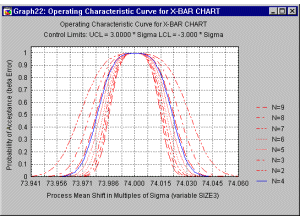 Кривые
операционных характеристик необычайно полезны
для исследования мощности процедуры контроля
качества. На практике решение о размерах выборок
должно зависеть не только от стоимости
реализации такого экспериментального плана
(например от стоимости изучения каждого
выборочного изделия), но также и от величины
потерь, возникающих при не обнаружении проблем с
качеством продукции. Кривая операционных
характеристик позволяет инженеру оценить
вероятность не обнаружения отклонений
определенной величины в качестве продукции.
Кривые
операционных характеристик необычайно полезны
для исследования мощности процедуры контроля
качества. На практике решение о размерах выборок
должно зависеть не только от стоимости
реализации такого экспериментального плана
(например от стоимости изучения каждого
выборочного изделия), но также и от величины
потерь, возникающих при не обнаружении проблем с
качеством продукции. Кривая операционных
характеристик позволяет инженеру оценить
вероятность не обнаружения отклонений
определенной величины в качестве продукции.
Для получения дополнительной информации см.
также раздел Кривые
операционных характеристик.
Кривые Пирсона. Система функций распределения, предложенная К. Пирсоном (см., Hahn and Shapiro, 1967, стр. 220-224) содержит 7 решений (из 12 первоначально введенных Пирсоном) дифференциального уравнения, которые аппроксимируют широкий набор распределений различной формы. Gruska, Mirkhani, and Lamberson (1989) подробно описали, как различные типы кривых Пирсона могут быть подогнаны к эмпирическому распределению. Метод вычисления процентных точек распределений Пирсона также описан у Davis and Stephens (1983).
См. также кривые Джонсона.
Критерии однородности дисперсии Левена и Брауна-Форсайта. Важным предположением дисперсионного анализа (см. Дисперсионный анализ и t-критерий для разности средних) является предположение об однородности дисперсии в различных группах. Наиболее часто для проверки этого предположения используются два достаточно мощных критерия: критерий Левена и его модификация, предложенная Брауном-Форсайтом. Однако важно понимать, что (1) предположение однородности дисперсии не так критично, как другие предположения дисперсионного анализа, в частности, в случае сбалансированных планов (с равным числом наблюдений n, см. также Дисперсионный анализ: однородность дисперсии и ковариации), а также, что (2) описанные ниже критерии сами по себе не обязательно являются очень устойчивыми (робастными) (например, в работе Glass and Hopkins, 1996, стр. 436, эти критерии называются "фатально недоработанными"; см. также описание этих критериев). Если вас беспокоит выполнение критерия однородности дисперсии, всегда полезно повторить некоторые ключевые моменты анализа с помощью непараметрических методов.
Критерий Левена однородности дисперсии: Для каждой зависимой переменной, проводится дисперсионный анализ абсолютных отклонений наблюдаемых значений от соответствующих средних по группам. Если критерий Левена является статистически значимым, гипотеза об однородности дисперсии должна быть отвергнута.
Критери Брауна-Форсайта однородности
дисперсии: Совсем недавно некоторые авторы
(см., например, работу Glass and Hopkins, 1996) затронули
вопрос о мощности критерия Левена для неравных
дисперсий. А именно, наиболее вероятное
распределение абсолютных отклонений (от
внутригрупповых средних) сильно асимметрично;
поэтому предположение дисперсионного анализа о
нормальности абсолютных отклонений обычно
нарушается. Это создает проблемы при сравнении
двух или нескольких групп с неравными объемами
выборок. В работе Brown and Forsythe (1974) был предложен
боле робастный критерий, по своей структуре
очень похожий на критерий Левена. Вместо
проведения дисперсионного анализа отклонений от
средних, можно провести анализ отклонений от
медиан по группам. В работе Olejnik and Algina (1987) было
показано, что уровень ошибки этого критерия
достаточно точно предсказуем даже при значимых
отклонениях от предположения о нормальности. Тем
не менее, как отмечается в работе Glass and Hopkins (1996,
стр. 436), оба критерия - критерия Левена и его
модификация Брауна-Форсайта обладают общим
недостатком, который авторы называют
"фатальной недоработкой", а именно,оба
критерия основываются на предположении об
однородности дисперсии (абсолютных отклонений
от средних или медиан); и, следовательно, не ясно,
насколько робастны эти критерии к присутствию
значимой неоднородности дисперсии и
несовпадающим объемам выборок.
Критерии серий (для контрольных карт). Эти критерии предназначены для обнаружения измерений, которые могут служить индикаторами того, что процесс вышел из-под контроля. Если выборочные точки (например, среднее в X-карте) попадают за контрольные пределы, имеет смысл считать, что процесс более не контролируем. Дополнительно находятся систематическое расположение точек (например, средние) между выборками, указывающие на сдвиг среднего. Модуль Интерактивные карты контроля качества предлагает (дополнительно) стандартный набор тестов для выявления определенного расположения данных, указывающих на выход процесса из-под контроля так называемые AT&T правила серий (see AT&T, 1959) или тесты для специальных причин (см. Nelson, 1984, 1985; Grant and Leavenworth, 1980; Shirland, 1993). Термин специальные (special или assignable) причины, как противоположный случайным или общим причинам, введены Shewhart, чтобы различить процесс, который находится под воздействием только случайных причин, и процесс, который выходит из-под контроля вследствие неслучайных или специальных факторов (см. Montgomery, 1991, p. 102).
Критерии серий имеют "статистическое" обоснование. Так, например, вероятность того, что любое выборочное среднее значение для X-карты окажется выше центральной линии, равна 0.5 при следующих условиях: (1) производственный процесс находится в нормальном состоянии (т.е. центральная линия проведена через значение, равное среднему контролируемой характеристики генеральной совокупности изделий), (2) средние значения следующих друг за другом выборок независимы (т.е. отсутствует автокорреляция) и (3) выборочные средние значения контролируемой характеристики распределены по нормальному закону. Проще говоря, при таких условиях для выборочного среднего значения шансы попасть выше или ниже центральной линии составляют 50 на 50. Поэтому вероятность того, что два следующих друг за другом выборочных средних окажутся выше центральной линии, будет равна 0.5, умноженному на 0.5 , т.е. 0.25.
Дополнительную информацию см. в Критерии серий; см. также Специальные причины.
Критерий Андерсона-Дарлинга. Критерий Андерсона-Дарлинга является общим критерием согласия эмпирической (оцененной) функции распределения с ожидаемой или гипотетической. Этот критерий применяется к данным без цензурирования (см. цензурирование). Критические значения статистики Андерсона-Дарлинга табулированы для объмов выборки от 10 до 40 (см., например, Dodson, 1994, Table 4.4); этот критерий не вычисляется для объема выборки n меньше 10 и больше 40.
Критерий Андерсона-Дарлинга используется в Анализе Вейбулла и анализе
надежности/времен отказа; см. также Манна критерий и Холландера-Прошана
критерий.
Критерий Манна. Этот критерий предложен Mann, Scheuer, Fertig (1973) и описан детально, например, в Dodson (1994) или Lawless (1982). Нулевая гипотеза, проверяемая критерием, утверждает что данные имеют распределение Вейбулла с оцененными параметрами. Nelson (1982) отмечает, что критерий имеет хорошую мощность и может применяться к Цензурированию типа II. Вычислительные детали даны в Dodson (1994) или в Lawless (1982). Критические значения рассчитаны методом Монте-Карло и табулированы для выборок объема от 3 до 25; для объемов выборки больше 25 критерий не вычисляется.
Критерий Манна используется в Анализе Вейбулла и анализе
надежности/времен отказа; см. также Холлендера-Прошана
критерий и Андерсона-Дарлинга
критерий.
Критерий Холландера-Прошана. Этот критерий сравнивает теоретическую функцию надежности с оценкой Каплана-Мейера. Формула для вычисления достаточно сложна, см. например, Dodson (1994, Chapter 4). Критерий можно применять как для однократного цензурирования, так и для многократного цензурирования; однако Dodson (1994) отмечает, что критерий иногда показывает малую мощность, когда данные грубо однократно цензурированы. Критерий Холландера-Прошана C можно использовать для проверки отсутствия согласия распределения с нормальным распределением (z).
Критерий Холландера-Прошана используется в Анализе Вейбулла и анализе
надежности/времен отказа; см. также Манна критерий и Андерсона-Дарлинга критерий.
Кросс-проверка. Кросс-проверка представляет собой процедуру оценки точности прогнозирования с помощью данных из специальной тестовой выборки (используется также термин кросс-проверочная выборка) путем сравнения точности прогноза с той, что достигается на обучающей выборке, то есть на выборке, по которой собственно строилась модель. Итак, модель строится по обучающей выборке, а точность прогноза на основании модели оценивается по тестовой выборке. В идеале, когда имеется достаточно большая выборка, часть наблюдений (например, половину или две трети) можно использовать для обучающей выборки, а оставшиеся наблюдения - для тестовой. Если на тестовой выборке модель дает результаты того же качества, что и на обучающей выборке, то говорят, что модель хорошо прошла кросс-проверку. Подробнее о кросс-проверке на тестовой выборке см. раздел Вычислительные методы главы Деревья классификации, раздел Классификация главы Дискриминантный анализ, а также главу Добыча данных.
Для выполнения кросс-проверки при малых
объемах выборки разработаны специальные методы,
в которых тестовая и обучающая выборки
могут частично пересекаться. О некоторых методах
такого типа рассказано в разделе Вычислительные методы
главы Деревья классификации.
Кросс-проверка
(для нейронных сетей). То же самое, что и
вообще кросс-проверка.
Применительно к нейронным сетям заключается в
использовании во время итерационного обучения
дополнительного множества данных (контрольного
множества). В то время как обучающее множество
используется для корректировки весов сети,
контрольное множество служит для независимой
проверки того, как нейронная
сеть научилась обобщать информацию.
Кросстабуляция (таблицы сопряженности, многовходовые таблицы). Кросстабуляция - это процесс объединения двух (или нескольких) таблиц частот так, что каждая ячейка (клетка) таблицы представляется единственной комбинацией значений или уровней табулированных переменных. Таким образом, кросстабуляция позволяет совместить частоты появления наблюдений на разных уровнях рассматриваемых факторов. Следующая таблица отчетливо показывает сильную связь между двумя переменными: Возрастом (Взрослый или Ребенок) и любимым сортом Печенья (сорт A или сорт B).
| ПЕЧЕНЬЕ: A | ПЕЧЕНЬЕ: B | ||
|---|---|---|---|
| ВОЗРАСТ: ВЗРОСЛЫЙ | 50 | 0 | 50 |
| ВОЗРАСТ: РЕБЕНОК | 0 | 50 | 50 |
| 50 | 50 | 100 |
Из таблицы видно, что все взрослые выбирают печенье A, а все дети - печенье B. Исследуя эти частоты, можно определить связи между табулированными переменными. Обычно кросстабулируются только группирующие (номинальные) переменные или переменные с относительно небольшим числом значений. Если вы хотите кросстабулировать непрерывную переменную (например, доход), то вначале ее следует перекодировать , разбив диапазон изменения на небольшое число интервалов (например, доход низкий, средний, высокий).
За дополнительной информацией обратитесь к
разделу Таблицы
сопряженности главы Основные
статистики.
Кросс-энтропия (для нейронных сетей). Функция ошибок, основанная на теоретико-информационных характеристиках. Особенно хорошо подходит для задач классификации. Имеется два варианта: для сетей с одним выходом и для сетей с несколькими выходами; в первом варианте используются логистические функции активации, во втором - функции софтмакс (Bishop, 1995).
См. также нейронные сети.
Круговая диаграмма - Значения. Последовательность значений переменной изображается в виде последовательных круговых секторов (термин "круговая диаграмма" был впервые использован Хаскеллом в 1922 г.); размер каждого сектора пропорционален соответствующему значению. Значения должны быть больше 0 (нулевое и отрицательные значения не могут быть представлены в виде круговых секторов). Этот простой тип круговой диаграммы (иногда называемый круговой диаграммой данных) интерпретирует данные самым непосредственным образом: одно наблюдение соответствует одному сектору.

См. также Круговые диаграммы.
Круговая диаграмма - Многоцветная столбчатая диаграмма. Многоцветная столбчатая диаграмма служит для изображения того же типа данных, что и круговая диаграмма значений (см. Круговая диаграмма - Значения или 2М гистограммы); однако последовательные значения выражены высотами вертикальных столбцов (разных цветов и видов), а не площадями круговых секторов.

Преимущество этих диаграмм перед круговыми диаграммами состоит в том, что они дают возможность более точного сравнения представленных значений (например, трудно сравнивать маленькие круговые секторы, если они не являются соседними). Этот тип графика может также иметь преимущества перед простыми гистограммами (где для всех столбцов используется один цвет и шаблон заполнения) в случаях, когда требуется быстрая идентификация определенных столбцов.
См. также Круговые диаграммы.
Круговая диаграмма - Частоты. В отличие от круговой диаграммы значений этот тип круговых диаграмм (термин был впервые использован Хаскеллом в 1922 г.), иногда называемый частотной круговой диаграммой, интерпретирует данные так же, как и гистограмма. Все значения выбранной переменной категоризуются по выбранному методу категоризации, а затем относительные частоты изображаются в виде круговых секторов соответствующих размеров.

См. также Круговые диаграммы.