Избыточностьправ = [
Канонический анализ
Вводный обзор
Во многих модулях STATISTICA можно вычислить парные коэффициенты корреляции для выражения зависимости между двумя переменными. Можно также вычислить матрицы парных коэффициентов корреляции. Например, коэффициент корреляции Пирсона (r) показывает степень линейной зависимости двумя переменными, измеренными в интервальной шкале. Модуль Непараметрическая статистика и распределения предлагает различные статистики, основанные на рангах исследуемых переменных. Модуль Множественная регрессия позволяет оценить зависимость между зависимой переменной (откликом) и множеством предикторных переменных. Модуль Многомерный анализ соответствий позволяет исследовать зависимости внутри множества категориальных переменных.
Модуль Каноническая корреляция
предназначен для анализа зависимостей между
списками переменными. Если говорить точнее, он
позволяет исследовать зависимость между двумя
множествами переменных, и в этом смысле он
развивает возможности других модулей. Например,
исследователь в сфере образования может оценить
зависимость между навыками по трем учебным
дисциплинам и оценками по пяти школьным
предметам. Социолог может исследовать
зависимость между прогнозами социальных
изменений, печатаемыми в двух газетах, и
реальными изменениями, оцененными с помощью
четырех различных статистических признаков.
Медик может изучить зависимость между
различными неблагоприятными факторами и
появлением определенной группы симптомов
заболевания. Во всех этих случаях нас интересует
зависимость между двумя множествами переменных,
для анализа которой и предназначен модуль Каноническая
корреляция.
В следующих разделах мы кратко познакомим вас с
основными идеями канонического анализа
корреляции. Предполагается, что вы уже знакомы с
обычным коэффициентом корреляции, описанным в
разделе Основные статистики и
таблицы, а также имеете общее представление
о множественной регрессии, описанной во Вводном обзоре раздела
Множественная регрессия.
| В начало |
Вычислительные методы и результаты
Далее мы рассмотрим использование некоторых вычислительных методов и дадим пояснение основным получаемым результатам.
Собственные значения. При вычислении канонических корней STATISTICA подсчитывает собственные значения матрицы корреляций. Эти значения равны доле дисперсии, объясняемой корреляцией между соответствующими каноническими переменными. При этом полученная доля вычисляется относительно дисперсии канонических переменных, т.е. взвешенных сумм по двум множествам переменных; таким образом, собственные значения не показывают абсолютного значения, объясняемого в соответствующих канонических переменных. При проведении анализа программа вычислит столько собственных значений, сколько имеется канонических корней, т.е. столько, сколько переменных имеется в наименьшем множестве.
Последовательно вычисляемые собственные
значения будут все меньшего и меньшего размера.
На первом шаге программа вычисляет веса,
максимизирующие корреляцию между взвешенными
суммами по двум множествам и определяет
соответствующее им значение первого корня.
Далее, на каждом шаге, программа находит
следующую пару канонических переменных, имеющих
максимальную корреляцию и не
коррелированных с предыдущими парами, и
вычисляет соответствующее ей значение
канонического корня.
Канонические корреляции. Если извлечь квадратный корень из полученных собственных значений, получим набор чисел, который можно проинтерпретировать как коэффициенты корреляции (см. также разделе Основные статистики и таблицы). Поскольку они относятся к каноническим переменным, их также называют каноническими корреляциями. Как и собственные значения, корреляции между последовательно выделяемыми на каждом шаге каноническими переменными, убывают. Поэтому, в выводимом на экран отчете о коррелированности между множествами переменных часто приводят лишь первое, т.е. максимальное значение. Однако другие канонические переменные также могут быть значимо коррелированы, и эти корреляции часто допускают достаточно осмысленную интерпретацию.
Значимость корней. Критерий значимости канонических корреляций сравнительно несложен. Во-первых, канонические корреляции оцениваются одна за другой в порядке убывания. Только те корни, которые оказались статистически значимыми, оставляются для последующего анализа. Хотя на самом деле вычисления происходят немного иначе. Программа сначала оценивает значимость всего набора корней, затем значимость набора, остающегося после удаления первого корня, второго корня, и т.д.
Некоторые авторы подвергали критике
использование последовательных критериев
значимости для канонических корней (см.,
например, работу Harris, 1976). Однако, эта процедура
была "реабилитирована" с помощью метода
Монте-Карло в вышедшей позднее книге Mendoza, Markos and
Gonter (1978).
Исследования показали, что используемый
критерий обнаруживает большие канонические
корреляции даже при небольшом размере выборки
(например, n = 50). Слабые канонические корреляции
(например, R = .3) требуют больших размеров выборки
(n > 200) для обнаружения в 50% случаев. Отметим, что
канонические корреляции небольшого размера
обычно не представляют практической ценности,
поскольку им соответствует небольшая реальная
изменчивость исходных данных. Чуть позднее, мы
поговорим об этом подробнее, а также обсудим
влияние на результаты размера выборки.
Канонические веса. После определения числа значимых канонических корней возникает вопрос об интерпретации каждого (значимого) корня. Напомним, что каждый корень в действительности представляет две взвешенные суммы, по одной на каждое множество переменных. Одним из способов толкования "смысла" каждого канонического корня является рассмотрение весов, сопоставленных каждому множеству переменных. Эти веса также называются каноническими весами.
При анализе, обычно, пользуются тем, что чем
больше приписанный вес (т.е., абсолютное значение
веса), тем больше вклад соответствующей
переменной в значение канонической переменной.
Для проведения более подробного сравнительного
анализа обычно рассматриваются
стандартизованные переменные, т.е.
z-преобразованные переменные с
нулевым средним и единичным стандартным
отклонением.
Если вы знакомы с множественной регрессией, вы можете применить для канонических весов интерпретацию, использованную для бета - весов в уравнении множественной регрессии. Канонические веса, в некотором смысле, аналогичны частным корреляциям переменных, соответствующих каноническому корню. Если вы знакомы с факторным анализом, то можете интерпретировать канонические веса аналогично весовым коэффициентам факторов. Таким образом, рассмотрение канонических весов позволяют понять "значение" каждого канонического корня, т.е. увидеть, как конкретные переменные в каждом множестве влияют на взвешенную сумму (т.е. каноническую переменную).
Канонические значения. Канонические
веса также могут использоваться для вычисления
значений канонических переменных. Для этого
достаточно сложить исходные переменные с
соответствующими весовыми коэффициентами.
Напомним, что канонические веса обычно
определяются для стандартизированных (z -
преобразованных) переменных.
Факторная структура. Еще одним
способом интерпретации канонических корней
является рассмотрение обычных корреляций между
каноническими переменными (или факторами) и
переменными из каждого множества. Эти корреляции
также называются каноническими
нагрузками факторов. Считается, что переменные,
сильно коррелированные с канонической
переменной, имеют с ней много общего. Поэтому, при
описании смысла канонической переменной следует
исходить в основном из реального смысла этих
сильно коррелированных переменных. Такой
способ интерпретации канонических переменных
похож на метод, используемый в факторном
анализе.
Факторная структура и канонические веса.
Иногда канонические веса для переменной
оказываются близкими к нулю, а соответствующие
им нагрузки очень велики. Также возможна
обратная ситуация, когда канонические веса
велики, а нагрузки небольшие. В таких случаях
вывод может оказаться достаточно
противоречивым. Однако следует помнить, что
канонические веса соответствуют уникальному
вкладу каждой переменной, а нагрузки
канонических факторов представляют простые
суммарные корреляции. Например, пусть в наше
исследование удовлетворения от различных видов
деятельности мы включили два вопроса,
соответствующих примерно одному внешнему
фактору: (1) "Удовлетворены ли вы
отношениями с вашим руководителем
подразделения?" и (2) "Удовлетворены ли вы
отношениями с руководством?" Таким образом,
ответы на эти вопросы содержат излишнюю
информацию. Когда программа вычисляет веса для
взвешенных сумм (канонических переменных) по
каждому множеству, максимизируя их корреляцию,
ей потребуется включить в сумму только одну из
этих двух переменных. Если при этом больший вес
будет приписан первому ответу, вклад второго
ответа становится несущественным.
Следовательно, он получит нулевой или
пренебрежительно малый вес. Тем не менее, если вы
рассмотрите обычные корреляции между
соответствующими суммарными значениями и
значениями двух канонических переменных (т.е.
нагрузки факторов), они могут оказаться
существенными у обоих факторов. Таким образом,
еще раз повторим, что канонические значения
соответствуют уникальному вкладу вносимому
соответствующей переменной во взвешенную сумму
или каноническую переменную; нагрузки
канонических факторов отражают полную
корреляцию между соответствующей переменной
и взвешенной суммой.
Извлеченная дисперсия. Коэффициенты канонической корреляции соответствуют корреляции между взвешенными суммами по двум множествам переменных. Они не говорят ничего о том, какую часть изменчивости (дисперсии) каждый канонический корень объясняет в переменных. Однако, вы можете сделать заключение о доле объясняемой дисперсии, рассматривая нагрузки канонических факторов. Напомним, что они представляют собой корреляции между каноническими переменными и исходными переменными в соответствующем множестве. Если вы возведете эти корреляции в квадрат, полученные числа будут отражать долю дисперсии, объясняемую каждой переменной. Для каждого корня вы можете вычислить среднее значение этих долей. При этом получится средняя доля изменчивости объясненной в этом множестве на основании соответствующей канонической переменной. Другими словами, вы можете вычислить среднюю долю дисперсии, извлеченной каждым корнем.
Избыточность. Каноническая корреляция при возведении в квадрат дает долю дисперсии, общей для сумм по каждому множеству (канонической переменной). Если вы умножите эту долю на долю извлеченной дисперсии, вы получите меру избыточности множества переменных, т.е., величину, показывающую, насколько избыточно одно множество переменных, если задано другое множество. Избыточность может быть записана следующим образом:
Избыточностьлев = [![]() (нагрузкилев2)/p]*Rc2
(нагрузкилев2)/p]*Rc2
Избыточностьправ = [![]() (нагрузкиправ2)/q]*Rc2
(нагрузкиправ2)/q]*Rc2
В этих уравнениях, p обозначает число переменных в первом (левом) множестве переменных, а q число переменных во втором (правом) множестве. Величина Rc2 соответствует квадрату соответствующей канонической корреляции.
Отметим, что вы можете вычислить избыточность первого (левого) множества переменных при заданном втором (правом) множестве, и избыточность второго (правого) множества переменных при заданном первом (левом) множестве. Поскольку последовательно извлекаемые канонические корни не коррелированны между собой, то вы можете просто просуммировать избыточности по всем (или только по значимым) корням, получив при этом общий коэффициент избыточности (как предлагается в работе Stewart and Love, 1968).
Практическая значимость. Для измерения избыточности также бывает полезным определение практической значимости канонических корней. При больших размерах выборки (см. ниже), канонические корреляции со значением R = .30 могут оказаться статистически значимыми (см. выше). Если возвести этот коэффициент в квадрат (R-квадрат = .09) и использовать формулу для избыточности, становится ясным, что такие канонические корни объясняют лишь незначительную долю изменчивости переменных. Хотя, разумеется, окончательное решение о практической значимости принимается на основании субъективной позиции исследователя. Однако для получения правдоподобных оценок того, насколько реальная изменчивость переменных объясняется конкретным каноническим корнем, бывает полезным не забывать о мере избыточности, т.е., о том насколько реальная изменчивость в одном множестве переменных объясняется другим множеством.
| В начало |
В этом разделе приводится список наиболее важных предположений анализа канонической корреляции, выполнение которых обеспечивает получение достоверных и обоснованных результатов.
Распределение. Применение критерия значимости при анализе канонической корреляции основано на предположении, что переменные в выборке имеют многомерное нормальное распределение. Как и большинство других модулей пакета STATISTICA, модуль Каноническая корреляция позволяет провести графический анализ данных, т.е., построить гистограмму частот с наложенной на нее нормальной кривой, или вывести на экран диаграмму рассеяния наблюдаемой переменной. Теоретически, последствия нарушения этого предположения мало изучены. Однако при очень больших размерах выборки (см. ниже) результаты анализа канонической корреляции достаточно устойчивы или робастны.
Объем выборки. В книге Stevens (1986)
приводится подробное обсуждение размера
выборки, необходимого для получения достоверных
результатов. Как уже говорилось, при наличии
больших корреляций между данными (например, R >
.7), даже малые размеры выборки (например, n = 50)
позволяют в большинстве случаев обнаружить эти
корреляции. Однако, для получения достоверных
оценок нагрузок канонических факторов (для
интерпретации), Стивенс рекомендует
использовать как минимум в 20 раз больше
наблюдений, чем число переменных, используемых в
анализе, если нужно интерпретировать только
наиболее значимый корень. Для получения
достоверных оценок
для двух канонических корней, в книге Barcikowski and
Stevens (1975) авторы рекомендуют, основываясь на
исследовании с помощью метода Монте-Карло,
использовать в 40 - 60 раз больше наблюдений, чем
число исследуемых переменных.
Выбросы. Наличие выбросов может оказывать большое влияние на значение коэффициентов корреляции (см. Основные статистики и таблицы). Поэтому выбросы могут оказывать заметное влияние на вычисление канонических корреляций. Конечно, чем больше размер выборки, тем меньшее значение оказывают один или два выброса. Однако при проведении анализа все-таки хорошо было бы построить диаграмму рассеяния (как показано на анимационном ролике внизу)
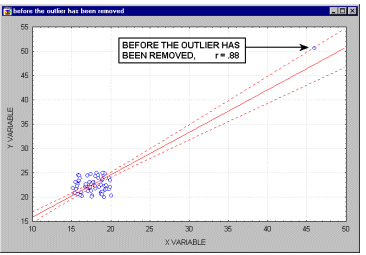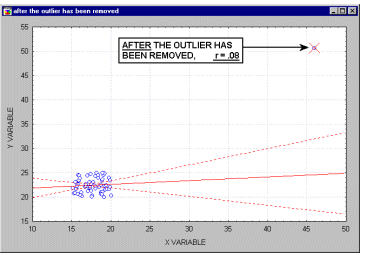
См. также Доверительный эллипс.
Плохо обусловленные матрицы. Еще одним предположением является требование, чтобы переменные в обоих множествах не были полностью избыточным. Например, если включить одну и ту же переменную дважды в одно из множеств, то окажется непонятным, какие ей следует придать веса. С вычислительной точки зрения, такая избыточность нарушает ход анализа. При наличии полной коррелированности между наблюдаемыми переменными (R = 1.0) корреляционная матрица не может быть обращена, и вычисления, необходимые для анализа канонической корреляции, таким образом, не могут быть завершены. Подобные корреляционные матрицы называются плохо обусловленными.
Таким образом, смысл этого предположения достаточно прост. Однако, при анализе большого количества сильно избыточных переменных, как бывает при анализе ответов в массовых опросах, оно зачастую "почти" нарушается.
| В начало |
Основные идеи
В качестве примера использования анализа канонических корреляций рассмотрим исследование анкет некоторого опроса. Анкетируемые оценивали свое удовлетворение от выполняемой ими работы, отвечая на три вопроса, а также удовлетворение от деятельности в других сферах, отвечая еще на семь вопросов. Нам хотелось бы понять, как связано удовлетворение от работы с удовлетворением, получаемым в другой сфере жизни.
Суммы значений
Проще всего просуммировать значения откликов по двум множествам вопросов и посчитать корреляцию полученных сумм. Если полученная корреляция статистически значима, можно заключить, что существует зависимость между удовлетворением от работы и удовлетворением в других сферах.
Следует, однако, заметить, что это достаточно поспешное заключение. Ведь мы так ничего и не узнали о связи удовлетворения в конкретных сферах и удовлетворения от работы. По сути дела, упрощая задачу и суммируя отклики, мы, в общем случае, теряем важную информацию. Например, если значения двух откликов второго множества соответствуют удовлетворению от отношений с супругом и удовлетворению от финансового положения, то складывать их все равно, что складывать яблоки с апельсинами. Таким образом, мы заранее предположили, что материально обеспеченный человек, имеющий проблемы в отношениях с супругом, в целом сравним с необеспеченным, но счастливым в личной жизни человеком. Скорее всего, психологический портрет человека не настолько прост...
Проблема заключается в том, что, просто вычисляя корреляцию сумм по множествам, мы теряем важную информацию, и, возможно, просто "разрушаем" существующие зависимости между переменными, складывая "яблоки с апельсинами".
Использование взвешенных сумм. Для исправления положения разумно немного изменить изучаемые объекты. Вместо рассмотрения обычных сумм по множествам, полезно рассматривать взвешенные суммы, чтобы веса, приписанные отдельным слагаемым, соответствовали реальной "структуре" переменных, т.е. их взаимной значимости. Например, если на удовлетворение, получаемое от работы, мало влияет удовлетворение от отношений с супругом, но сильно влияет удовлетворение от материального положения, первому следует придать меньший вес, чем второму. Эту общую идею можно выразить следующим уравнением:
a1*y1 + a2*y2 + ... + ap*yp = b1*x1 + b2*x2 + ... + bq*xq
Таким образом, если у нас имеется два множества, содержащие p и q переменных соответственно, мы будем исследовать зависимость между взвешенными суммами переменных из каждого множества (т.е., между линейными комбинациями p и q переменных соответственно).
Определение весов. После того, как мы сформулировали в общем виде "уравнение модели" для канонической корреляции, нам осталось только определить веса для двух наборов переменных. Взвешенные суммы, слабо коррелированные друг с другом, не представляют никакого интереса для исследователя, поэтому при подборе весовых коэффициентов мы будем исходить из условия максимальной коррелированности двух множеств.
| В начало |
Используя терминологию анализа канонической
корреляции, можно сказать, что взвешенные суммы
определяют канонический корень или каноническую
переменную. Эти канонические переменные
(взвешенные суммы) можно рассматривать как
обозначения некоторых "скрытых" переменных,
лежащих в основе наблюдаемых явлений. Например,
если для второго рассматриваемого множества
факторов (связанного с получением
удовлетворения от различных сфер деятельности),
мы получим взвешенную сумму с большими весами
для факторов, относящихся к удовлетворению от
работы, то можем заключить, что соответствующая
каноническая переменная измеряет
удовлетворение от
работы.
Число корней
До сих мы предполагали, что для двух наборов переменных имеется ровно одна пара канонических переменных (взвешенных сумм). Однако, возможно, что множество факторов, касающихся удовлетворения от работы содержит факторы, связанные с удовлетворением размером заработной платы и отношениями с коллегами по работе. Тогда логично допустить, что удовлетворенность размером заработной платы коррелированна с удовлетворенностью материальным положением, а удовлетворенность отношениями с коллегами по работе коррелированна с удовлетворенностью отношениями с супругом. В таком случае полезно рассмотреть две дополнительные взвешенные суммы, отражающие сложность структуры исследуемых данных.
В действительности, канонический анализ
практически всегда приводит к вычислению более
чем одной пары взвешенных сумм. Если быть точным,
число канонических корней вычисляемых
программой равно числу переменных в меньшем
множестве. В нашем примере, когда анализируемые
группы содержали три и семь переменных
соответственно, число канонических корней будет
равно трем.
Как мы уже отметили, при вычислении корней программа рассматривает все максимально коррелированные взвешенные суммы (максимизирует значение корреляции между каноническими переменными). При вычислении более чем одного корня каждая последующая пара канонических переменных объясняет свою уникальную долю изменчивости в этих двух наборах переменных. При этом последовательно получаемые пары канонических переменных не коррелированны друг с другом и объясняют все меньшую и меньшую долю изменчивости.
| В начало |
![]()
© Copyright StatSoft, Inc., 1984-1998
STATISTICA является торговой маркой StatSoft, Inc.