Анализ выживаемости

Анализ выживаемости

Общие цели

Статистические методы, представленные в этом модуле, первоначально были развиты в медицинских, биологических исследованиях и страховании, но затем стали широко применяться в социальных и экономических науках, а также в инженерных задачах (анализ надежности и времен отказов).

Представьте, что вы изучаете эффективность нового метода лечения, применяемого в критической (терминальной) стадии заболевания (например, лечение новым методом практически неизлечимых больных). Наиболее важной, очевидно, переменной является продолжительность жизни пациентов с момента поступления в клинику. В принципе, для описания средних времен жизни и сравнения нового метода лечения со старыми, можно было бы использовать стандартные параметрические и непараметрические методы (см. Основные статистики и таблицы и Непараметрические статистики и распределения). Однако в анализируемых данных есть существенная особенность, связанная с тем, как вы строите выборку. При завершении вашего исследования могли найтись пациенты, которые выжили в течение всего периода наблюдения, в частности, среди тех, кто поступил в клинику позже других, а также пациенты, контакт с которыми был потерян до завершения эксперимента (например, их перевели в другие клиники). Естественно, вам не хотелось бы терять собранную о них информацию, поскольку большинство этих пациентов являются "выжившими" в течение того времени, которое вы их наблюдали, и тем самым свидетельствуют в пользу нового метода лечения. Наблюдения, которые содержат неполную информацию, называются цензурированными наблюдениями (например, "пациент A был жив, по крайней мере, 4 месяца до того, как был переведен в другую клинику и контакт с ним был потерян"). Использование в том числе и цензурированных наблюдений составляет специфику рассматриваемых здесь методов (термин цензурирование был впервые использован в работе Hald, 1949).

В начало

Цензурированные наблюдения

В общем, цензурированные наблюдения типичны, когда наблюдаемая величина представляет время до наступления некоторого критического события, а продолжительность наблюдения ограничена по времени. Цензурированные наблюдения встречаются во многих областях. Например, в социальных науках мы можем изучать "длительность" брака, интенсивность выбытия студентов из высшего учебного заведения (времен до выбытия), динамику численности работников в некоторых организациях и т.п. В рассмотренных примерах в конце периода наблюдения некоторые субъекты остаются состоящими в браке, некоторые студенты продолжают учебу, а некоторые сотрудники продолжают работать в компании; таким образом, данные об этих субъектах являются цензурированными. Мы не можем дождаться того момента, когда все выбранные студенты покинут учебное заведение, а сотрудники компанию.

В экономике мы можем изучать "выживание" новых предприятий или времена "жизни" продуктов, таких как, например, автомобили. В задачах контроля качества типичным является изучение "выживания" элементов изделий под нагрузкой (анализ времен отказов). В актуарной математике в качестве объекта исследований обычно используют таблицы смертности, содержащие данные о смертности за выбранные интервалы времени лиц определенных категорий (например, мужчин старше 30 лет).

В начало

Аналитические методы

Методы Анализа выживаемости в основном применяются к тем же статистическим задачам, что и другие методы, однако их особенность в том, что они применяются к цензурированным или, как иногда говорят, неполным данным. Отметим также, что более часто, чем обычная функция распределения, в этих методах используется так называемая функция выживания, представляющая собой вероятность того, что объект проживет время больше t. Построение таблиц времен жизни, подгонка распределения выживаемости, оценивание функции выживания с помощью процедуры Каплана-Мейера являются описательными методами исследования цензурированных данных. Некоторые из предложенных методов позволяют сравнивать выживаемость в двух и более группах. Наконец, Анализ выживаемости содержит регрессионные модели для оценивания зависимостей между многомерными непрерывными переменными со значениями типа времена жизни.

В начало

Анализ таблиц времен жизни

Наиболее естественным способом описания выживаемости в выборке явлвется построение Таблиц времен жизни. Техника таблиц времен жизни - один из старейших методов анализа данных о выживаемости (времен отказов) (см., например, работы Berkson and Gage, 1950; Cutler and Ederer, 1958; Gehan, 1969). Такую таблицу можно рассматривать как "расширенную" таблицу частот. Область возможных времен наступления критических событий (смертей, отказов и др.) разбивается на некоторое число интервалов. Для каждого интервала вычисляется число и долю объектов, которые в начале рассматриваемого интервала были "живы", число и долю объектов, которые "умерли" в данном интервале, а также число и долю объектов, которые были изъяты или цензурированы в каждом интервале.

На основании этих величин вычисляются некоторые дополнительные статистики:

Число изучаемых объектов. Это число объектов, которые были "живы" в начале рассматриваемого временного интервала, минус половина числа изъятых или цензурированных объектов.

Доля умерших. Эта отношение числа объектов, умерших в соответствующем интервале, к числу объектов, изучаемых на этом интервале.

Доля выживших. Эта доля равна единице минус доля умерших.

Кумулятивная доля выживших (функция выживания). Это кумулятивная доля выживших к началу соответствующего временного интервала. Поскольку вероятности выживания считаются независимыми на разных интервалах, эта доля равна произведению долей выживших объектов по всем предыдущим интервалам. Полученная доля как функция от времени называется также выживаемостью или функцией выживания [точнее, это оценка функции выживания].

Плотность вероятности. Это оценка вероятности отказа в соответствующем интервале, определяемая таким образом::

F_i = (P_i-P_i+1) /h_i

где F_i - оценка вероятности отказа в i-ом интервале, P_i - кумулятивная доля выживших объектов (функция выживания) к началу i-го интервала, h_i - ширина i-ого интервала.

Функция интенсивности. Функция интенсивности (этот термин был впервые использован в работе Barlow, 1963) определяется как вероятность того, что объект, выживший к началу соответствующего интервала, откажет или умрет в течение этого интервала. Оценка функции интенсивности вычисляется как число отказов, приходящихся на единицу времени соответствующего интервала, деленное на среднее число объектов, доживших до момента времени, находящегося в середине интервала.

Медиана ожидаемого времени жизни. Это точка на временной оси, в которой кумулятивная функция выживания равна 0.5. Другие процентили (например, 25- и 75-процентиль или квартили) кумулятивной функции выживания вычисляются по такому же принципу. Отмети, что 50-процентиль (медиана) кумулятивной функции выживаемости обычно не совпадает с точкой выживания 50% выборочных наблюдений. (Совпадение происходит только когда за прошедшее к этому моменту время не было цензурированных наблюдений).

Объем выборки. Чтобы получить надежные оценки трех основных функций (функции выживания, плотности вероятности и функции интенсивности) и их стандартных ошибок на каждом временном интервале, рекомендуется использовать не менее 30 наблюдений.

В начало

Подгонка распределения

Общее знакомство. В общем случае таблица времен жизни дает хорошее представление о распределении отказов или смертей объектов во времени. Однако для прогноза часто необходимо знать форму рассматриваемой функции выживания. Наиболее важны следующие семейства распределений, которые используются для описания продолжительности жизни или наработки до отказа: экспоненциальное (в том числе, линейное экспоненциальное) распределение, распределение Вейбулла экстремальных значений и распределение Гомперца.

Оценивание. Процедура оценивания параметров использует алгоритм метода наименьших квадратов (см. работу Gehan and Siddiqui, 1973). Для проведения оценивания применима модель линейной регрессии, поскольку все четыре перечисленных семейства распределений могут быть "сведены к линейным" (относительно параметров) с помощью подходящих преобразований. Такие преобразования приводят иногда к тому, что дисперсия остатков зависит от интервалов (т.е. дисперсия различная на различных интервалах). Чтобы учесть это, в алгоритмах подгонки используют оценки взвешенных наименьших квадратов двух типов.

Согласие. Зная параметрическое семейство распределений, можно вычислить функцию правдоподобия по имеющимся данным и найти ее максимум. Такие оценки называются оценками максимального правдоподобия. При весьма общих предположениях эти оценки совпадают с оценками наименьших квадратов. Аналогичным образом находится максимум функции правдоподобия при нулевой гипотезе, т.е. для модели, допускающей различные интенсивности на разных интервалах. Сформулированная гипотеза может быть проверена, например, с помощью критерия отношения правдоподобия, статистика которого имеет (по крайней мере, асимптотически) хи-квадрат распределение.

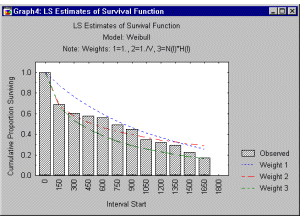
Графики. В модуле можно строить графики как эмпирических, так и теоретических функций распределения и интенсивности. Эти графики представляют собой прекрасное средство проверки согласия данных с теоретическим распределением. Ниже показана эмпирическая функция выживания и функции из семейства распределений Вейбулла.

График

На этом графике три линии обозначают теоретические распределения, полученнные с помощью трех различных процедур оценивания (методом наименьших квадратов и двумя методами взвешенных наименьших квадратов).

Множительные оценки Каплана-Мейера

Для цензурированных, но не группированных наблюдений времен жизни, функцию выживания можно оценить непосредственно (без таблицы времен жизни). Представьте, что вы создали файл, в котором каждое наблюдение содержит точно один временной интервал. Перемножая вероятности выживания в каждом интервале, получим следующую формулу для функции выживания:

S(t) = _j^t_=
1 [(n-j)/(n-j+1)]^{( j )}

В этом выражении S(t) - оценка функции выживания, n - общее число событий (времен окончания), j - порядковый (хронологически) номер отдельного события, d(j) равно 1, если j-ое событие означает отказ (смерть) и (j) равно 0, если j-ое событие означает потерю наблюдения (цензурирование). означает произведение по всем наблюдениям j, завершившимся к моменту t. Данная оценка функции выживания, называемая множительной оценкой, впервые была предложена Капланом и Мейером (1958).

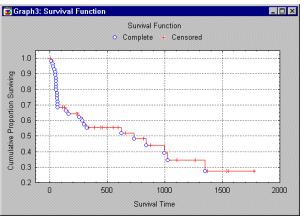
График

Преимущество метода Каплана-Мейера (по сравнению с методом таблиц жизни) состоит в том, что оценки не зависят от разбиения времени наблюдения на интервалы, т.е. от группировки. Метод множительных оценок и метод таблиц времен жизни приводят, по существу, к одинаковым результатам, если временные интервалы содержат, максимум, по одному наблюдению.

В начало

Сравнение выборок

Общее знакомство. Можно сравнить времена жизни или, на техническом языке, наработки до отказа нескольких выборок. В принципе, т.к. времена жизни не являются нормально распределенными, можно использовать непараметрические тесты, основанные на рангах. Непараметрические статистики предлагают широкий набор непараметрических критериев, которые могли бы быть применены для сравнения времен жизни; однако эти критерии не "работают" с цензурированными данными.

Доступные критерии. В Анализе выживаемости имеется пять различных (в основном непараметрических) критериев для цензурированных данных: обобщенный (Геханом) критерий Вилкоксона, F-критерий Кокса, логарифмический ранговый критерий, а также обобщенный Пето (Peto R.и Peto J.) критерий Вилкоксона. Большинство этих критериев приводят соответствующие z-значения (значения стандартного нормального распределения); эти z-значения могут быть использованы для статистической проверки любых различий между группами. Однако критерии дают надежные результаты лишь при достаточно больших объемах выборок. При малых объемах выборок их "поведение" менее поддается осмыслению.

Выбор двухвыборочного критерия. Не существует твердо установленных рекомендаций по применению определенных критериев. Однако известно, что F - критерий Кокса обычно более мощный, чем критерий Вилкоксона - Гехана, если:

выборочные объемы малы (то есть объем группы n меньше 50);
если выборки извлекаются из экспоненциального распределения или распределения Вейбулла;
если нет цензурированных наблюдений (см. работу Gehan and Thomas, 1969).

В работе Lee, Desu, and Gehan (1975) авторы сравнили критерий Гехана с некоторыми другими критериями и показали, что критерий Кокса-Ментела и логарифмически ранговый критерий являются более мощным (безотносительно к цензурированию), если выборки извлечены из экспоненциального распределения или распределения Вейбулла; при этих условиях между критерием Кокса-Ментела и логарифмически ранговым критерием почти нет различия. В работе Ли (Lee (1980)) обсуждается мощность различных критериев более детально. Если вас затрудняет выбор определенного критерия, мы рекомендуем обратиться к этим работам.

Критерий для нескольких выборок. Многовыборочный критерий представляет собой развитие критерия Вилкоксона, обобщенного Геханом, критерия Вилкоксона, обобщенного Пето, и логарифмически рангового критерия. Сначала каждому времени жизни приписывается его вклад в соответствии с процедурой Ментела (Mantel, 1967); далее на основе этих вкладов (по группам) вычисляется значение статистики хи-квадрат. Если выделены только две группы, то критерий эквивалентен критерию Вилкоксона, обобщенному Геханом.

Неравные доли цензурированных наблюдений. Если сравниваются две или более группы, то важно проверить доли цензурированных наблюдений в каждой. В частности, в медицинских исследованиях степень цензурирования может зависеть, например, от различий в методе лечения: пациенты, которым стало много лучше или стало хуже, с большой вероятностью теряются из наблюдения. Различие в степени цензурирования может привести к смещению в статистических выводах.

В начало

Регрессионные модели

Общее знакомство

Самая большая проблема медицинских, биологических или инженерных статистических исследований состоит в выяснении того, являются ли некоторые непрерывные переменные связанными с наблюдаемыми временами жизни. Есть две главные причины, по которым в таких исследованиях не может быть непосредственно применена классическая техника множественной регрессии (см. Множественная регрессия). Во-первых, времена жизни обычно не являются нормально распределенными, а это является серьезным нарушением предположений для оценивания множественной регрессии по методу наименьших квадратов. Времена жизни обычно имеют экспоненциальное распределение или распределение Вейбулла. Во-вторых имеется проблема с цензурированными, т.е. незавершенными наблюдениями.

Модель пропорциональных интенсивностей Кокса

Модель пропорциональных интенсивностей - наиболее общая регрессионная модель, поскольку она не связана с какими-либо предположениями относительно распределения времени выживания. Эта модель предполагает, что функция интенсивности имеет некоторый уровень y, являющийся функцией независимых переменных. Никаких предположений о виде функции интенсивности не делается. Поэтому модель Кокса может рассматриваться как в некотором смысле непараметрическая. Модель может быть записана в следующем виде:

h{(t), (z₁, z₂, ..., z_m)} = h₀(t)*exp(b₁*z₁ + ... + b_m*z_m)

где h(t,...) обозначает результирующую интенсивность, при заданных для соответствующего наблюдения значениях m ковариат (z₁, z₂, ..., z_m) и соответствующем времени жизни (t). Множитель h₀(t) называется базовой функцией интенсивности, она равна интенсивности в случае, когда все независимые переменные равны нулю. Можно линеаризовать эту модель, поделив обе части соотношения на h₀(t) и взяв натуральный логарифм от обеих частей:

log[h{(t), (z...)}/h₀(t)] = b₁*z₁ + ... + b_m*z_m

Теперь мы имеем достаточно "простую" линейную модель, которая легко поддается изучению.

Предположения. В то время как никаких прямых предположений о виде функции интенсивности ранее не делалось, модельное уравнение, приведенное выше, подразумевает два предположения. Во-первых, зависимость между функцией интенсивности и логлинейной функцией ковариат является мультипликативной. Это соотношение называется также предположением (гипотезой) пропорциональности. Реально оно означает, что для двух заданных наблюдений с различными значениями независимых переменных отношения их функций интенсивности не зависит от времени (чтобы ослабить это предположение, используются ковариаты, зависящие от времени; см. ниже). Второе предположение состоит именно в логарифмической линейности соотношения между функцией интенсивности и независимыми переменными.

Модель пропорциональных интенсивностей Кокса с зависящими от времени ковариатами

Обоснованность предположения пропорциональности интенсивности часто подвергается сомнению. Например, рассмотрим гипотетическое исследование, в котором ковариатой является категориальная (групповая) переменная, а именно, индикатор того, подвергнут некоторый пациент или нет хирургической операции. Пусть пациент 1 подвергнут операции, в то время как пациент 2 - нет. Согласно предположению пропорциональности отношение функций интенсивностей для обоих пациентов не зависит от времени и означает, что риск для пациента, подвергнутого операции, постоянно более высокий (или более низкий), чем риск пациента, не подвергнутого операции (при условии, что оба дожили до рассматриваемого момента). Однако обычно более реалистична другая модель, а именно: сразу после операции риск прооперированного пациента выше, однако при благоприятном исходе операции с течением времени убывает и становится меньше риска не оперированного пациента. В этом случае предпочтительнее ковариаты, зависящие от времени. Можно привести много других примеров, где предположение о пропорциональности неприемлемо. Так, при изучении физического здоровья возраст является одним из факторов выживаемости после хирургической операции. Ясно, что возраст - более важный предиктор для риска сразу после операции, чем по прошествии некоторого времени после операции (например, после первых признаков выздоровления). В ускоренных испытаниях на надежность иногда используют нагрузочную ковариату (например, уровень напряжения), которую медленно наращивают со временем вплоть до отказа прибора, например, до пробоя изоляции; см. Lawless, 1982, стр. 393). В этом случае влияние ковариаты опять зависит от времени.

Проверка предположения пропорциональности. Как отмечалось в предыдущих примерах, часто предположение пропорциональности не выполняется. В таком случае, можно явно определить ковариаты, как функции времени. Например, рассмотрим набор данных, представленных Pike (1966), который состоит из времен жизни двух групп крыс, одна из которых была контрольной, а другая была подвергнута воздействию канцерогена (см. также подобный пример в работе Lawless, 1982, стр. 393). Предположим, что z - групповая переменная со значениями 1 и 0 для подвергнутых воздействию и контрольных крыс соответственно. Тогда можно проводить подгонку функции интенсивности с помощью модели пропорциональных интенсивностей вида:

h(t,z) = h₀(t)*exp{b₁*z + b₂*[z*log(t)-5.4]}

Обратите внимание, что функция интенсивности в момент t есть функция: (1) базовой функции интенсивности h₀, (2) ковариаты z и (3) z-кратного логарифма времени. Заметим, что константа 5.4 использована здесь только как нормировка, т.к. среднее логарифма времени жизни для этого множества данных равно 5.4. Другими словами, структурированный моделью множитель с ковариатами в каждый момент времени есть функция ковариаты и времени; таким образом, влияние ковариаты на выживаемость зависит от времени; отсюда название - ковариата, зависящая от времени. Эта модель позволяет использовать специфический критерий проверки предположения пропорциональности. Если параметр b₂ статистически значим (например, если он, по крайней мере, в два раза больше своей стандартной ошибки), то можно сделать вывод, что ковариаты z действительно зависят от времени, и поэтому предположение пропорциональности не выполняется.

Экспоненциальная регрессия

В своей основе эта модель предполагает, что распределение продолжительности жизни является экспоненциальным и связано со значениями некоторого множества независимых переменных (z_i). Параметр интенсивности экспоненциального распределения выражается в виде:

S(z) = exp(a + b₁*z₁ + b₂*z₂ + ... + b_m*z_m)

Здесь S(z) обозначает время жизни, a - константа, а b_i - параметры регрессии.

Согласие. Значение критерия хи-квадрат может быть вычислено как функция логарифма правдоподобия для модели со всеми оцененными параметрами (L₁) и логарифма правдоподобия модели, в которой все ковариаты обращаются в 0 (L₀). Если значение хи-квадрат статистически значимо, отвергаем нулевую гипотезу и принимаем, что независимые переменные значимо влияют на время жизни.

Стандартная экспоненциальная порядковая статистика. Один из способов проверки предположения экспоненциальности - построение остатков времен жизни и сравнение их со значениями стандартных экспоненциальных порядковых статистик альфа.

Нормальная и логнормальная регрессия

В этой модели предполагается, что времена жизни (или их логарифмы) имеют нормальное распределение. Модель в основном идентична обычной модели множественной регрессии и может быть описана следующим образом:

t = a + b₁*z₁ + b₂*z₂ + ... + b_m*z_m

Здесь t означает время жизни. Если принимается модель логнормальной регрессии, то t заменяется ln t. Модель нормальной регрессии особенно полезна, поскольку часто данные могут быть преобразованы в нормальные применением нормализующих аппроксимаций. Таким образом, в некотором смысле это наиболее общая параметрическая модель (в противоположность модели пропорциональных интенсивностей Кокса, которая является непараметрической), оценки которой могут быть получены для большого разнообразия исходных распределений времен жизни.

Согласие. Значение хи-квадрат может быть вычислено как функция логарифма правдоподобия для модели со всеми независимыми переменными (L₁) логарифма правдоподобия для модели, в которой все независимые переменные заменены 0 (L₀).

Стратифицированный анализ

Цель стратифицированного анализа - проверить гипотезу о том, что одна и та же регрессия является подходящей для разных групп (данных); то есть зависимость между выживаемостью и регрессорами одна и та же для разных групп данных. При стратифицированном анализе Анализ выживаемости вначале строит регрессионные модели отдельно для каждой группы. Сумма логарифмов правдоподобия для разных моделей представляет собой логарифм правдоподобия модели с разными коэффициентами регрессии (и свободными членами, если требуется) в разных группах. Далее программа подгоняет требуемую регрессионную модель ко всем данным обычным образом, не учитывая разбиение на группы, и вычисляет общий логарифм правдоподобия. По разности этих двух логарифмов правдоподобия проверяется статистическая значимость различия между группами (с точки зрения хи-квадрат статистики).