Дисперсионный анализ
Этот раздел содержит вводный обзор и обсуждение некоторых методов дисперсионного анализа, включая планы с повторными измерениями, ковариационный анализ, многомерный дисперсионный анализ, несбалансированные и вложенные планы, эффекты контрастов, апостериорные сравнения и др. Дополнительно, можно обратиться к разделу Компоненты дисперсии (разделы связанные с оцениванием компонент дисперсии в смешанных планах), Планирование эксперимента (разделы связанные со специальными областями применения дисперсионного анализа в промышленных условиях), а также Анализ повторяемости и воспроизводимости (разделы, относящиеся к оцениванию надежности и точности измерительных систем).
Основные идеи
Цель дисперсионного анализа.
Основной целью дисперсионного анализа является исследование значимости различия между средними. Раздел Элементарные понятия статистики содержит краткое введение в исследование статистической значимости. Если вы просто сравниваете средние в двух выборках, дисперсионный анализ даст тот же результат, что и обычный t-критерий для независимых выборок (если сравниваются две независимые группы объектов или наблюдений) или t-критерий для зависимых выборок (если сравниваются две переменные на одном и том же множестве объектов или наблюдений). Если вы не достаточно знакомы с этими критериями, рекомендуем обратиться к разделу Основные статистики и таблицы.
Откуда произошло название Дисперсионный анализ? Может показаться странным, что процедура сравнения средних называется дисперсионным анализом. В действительности, это связано с тем, что при исследовании статистической значимости различия между средними двух (или нескольких) групп, мы на самом деле сравниваем (т.е. анализируем) выборочные дисперсии. Фундаментальная концепция дисперсионного анализа предложена Фишером в 1920 году. Возможно, более естественным был бы термин анализ суммы квадратов или анализ вариации, но в силу традиции употребляется термин дисперсионный анализ.
Также смотрите разделы.
См. также Методы дисперсионного анализа, Компоненты дисперсии и смешанная модель ANOVA/ANCOVA, а также Планироване эксперимента.
Для выборки объема n выборочная дисперсия вычисляется как сумма квадратов отклонений от выборочного среднего, деленная на n-1 (объем выборки минус единица). Таким образом, при фиксированном объеме выборки n дисперсия есть функция суммы квадратов (отклонений), обозначаемая, для краткости, SS (от английского Sum of Squares - Сумма квадратов). Далее слово выборочная мы часто опускаем, прекрасно понимая, что рассматривается выборочная дисперсия или оценка дисперсии. В основе дисперсионного анализа лежит разделение дисперсии на части или компоненты. Рассмотрим следующий набор данных:
| Группа 1 | Группа 2 | |
|---|---|---|
| Наблюдение 1 Наблюдение 2 Наблюдение 3 |
2 3 1 |
6 7 5 |
| Среднее Сумма квадратов (СК) |
2 2 |
6 2 |
| Общее среднее Общая сумма квадратов |
4 28 |
|
Средние двух групп существенно различны (2 и 6 соответственно). Сумма квадратов отклонений внутри каждой группы равна 2. Складывая их, получаем 4. Если теперь повторить эти вычисления без учета групповой принадлежности, то есть, если вычислить SS исходя из общего среднего этих двух выборок, то получим величину 28. Иными словами, дисперсия (сумма квадратов), основанная на внутригрупповой изменчивости, приводит к гораздо меньшим значениям, чем при вычислении на основе общей изменчивости (относительно общего среднего). Причина этого, очевидно, заключается в существенной разнице между средними значениями, и это различие между средними и объясняет существующее различие между суммами квадратов. В самом деле, если использовать для анализа этих данных модуль Дисперсионный анализ, то будет получена следующая таблица, называемая таблицей дисперсионного анализа:
| ГЛАВНЫЙ ЭФФЕКТ | |||||
|---|---|---|---|---|---|
| SS | ст.св. | MS | F | p | |
| Эффект Ошибка |
24.0 4.0 |
1 4 |
24.0 1.0 |
24.0 |
.008 |
Как видно из таблицы, общая сумма квадратов SS =
28 разбита на компоненты: сумму квадратов,
обусловленную внутригрупповой
изменчивостью (2+2=4; см. вторую строку таблицы)
и сумму квадратов, обусловленную различием
средних значений между группами (28-(2+2)=24; см
первую строку таблицы). Заметим, что MS в этой
таблице есть средний квадрат, равный SS, деленная
на число степеней свободы (ст.св).
SS ошибок и SS эффекта. Внутригрупповая изменчивость (SS) обычно называется остаточной компонентой или дисперсией ошибки. Это означает, что обычно при проведении эксперимента она не может быть предсказана или объяснена. С другой стороны, SS эффекта (или компоненту дисперсии между группами) можно объяснить различием между средними значениями в группах. Иными словами, принадлежность к некоторой группе объясняет межгрупповую изменчивость, т.к. нам известно, что эти группы обладают разными средними значениями.
Проверка значимости. Основные идеи проверки статистической значимости обсуждаются в разделе Элементарные понятия статистики. В этом же разделе объясняются причины, по которым многие критерии используют отношение объясненной и необъясненной дисперсии. Примером такого использования является сам дисперсионный анализ. Проверка значимости в дисперсионном анализе основана на сравнении компоненты дисперсии, обусловленной межгрупповым разбросом (называемой средним квадратом эффекта или MSэффект) и компоненты дисперсии, обусловленной внутригрупповым разбросом (называемой средним квадратом ошибки или MSошибка; эти термины были впервые использованы в работе Edgeworth, 1885). Если верна нулевая гипотеза (равенство средних в двух популяциях), то можно ожидать сравнительно небольшое различие выборочных средних из-за чисто случайной изменчивости. Поэтому, при нулевой гипотезе, внутригрупповая дисперсия будет практически совпадать с общей дисперсией, подсчитанной без учета групповой принадлежности. Полученные внутригрупповые дисперсии можно сравнить с помощью F-критерия, проверяющего, действительно ли отношение дисперсий значимо больше 1. В рассмотренном выше примере F-критерий показывает, что различие между средними статистически значимо (значимо на уровне 0.008).
Основная логика дисперсионного анализа. Подводя итоги, можно сказать, что целью дисперсионного анализа является проверка статистической значимости различия между средними (для групп или переменных). Эта проверка проводится с помощью разбиения суммы квадратов на компоненты, т.е. с помощью разбиения общей дисперсии (вариации) на части, одна из которых обусловлена случайной ошибкой (то есть внутригрупповой изменчивостью), а вторая связана с различием средних значений. Последняя компонента дисперсии затем используется для анализа статистической значимости различия между средними значениями. Если это различие значимо, нулевая гипотеза отвергается и принимается альтернативная гипотеза о существовании различия между средними.
Зависимые и независимые переменные. Переменные, значения которых определяется с помощью измерений в ходе эксперимента (например, балл, набранный при тестировании), называются зависимыми переменными. Переменные, которыми можно управлять при проведении эксперимента (например, методы обучения или другие критерии, позволяющие разделить наблюдения на группы или классифицировать) называются факторами или независимыми переменными. Более подробно эти понятия описаны в разделе Элементарные понятия статистики.
Многофакторный дисперсионный анализ
В рассмотренном выше простом примере вы могли бы сразу вычислить t-критерий для независимых выборок, используя соответствующую опцию модуля Основные статистики и таблицы. Полученные результаты, естественно, совпадут с результатами дисперсионного анализа. Однако дисперсионный анализ содержит гораздо более гибкие и мощные технические средства, позволяющие исследовать планы практически неограниченной сложности.
Множество факторов. Мир по своей природе сложен и многомерен. Ситуации, когда некоторое явление полностью описывается одной переменной, чрезвычайно редки. Например, если мы пытаемся научиться выращивать большие помидоры, следует рассматривать факторы, связанные с генетической структурой растений, типом почвы, освещенностью, температурой и т.д. Таким образом, при проведении типичного эксперимента приходится иметь дело с большим количеством факторов. Основная причина, по которой использование дисперсионного анализа предпочтительнее повторного сравнения двух выборок при разных уровнях факторов с помощью серий t-критерия, заключается в том, что дисперсионный анализ существенно более эффективен и, для малых выборок, более информативен. Вам нужно сделать определенные усилия, чтобы овладеть техникой дисперсионного анализа, реализованной на STATISTICA, и ощутить все ее преимущества в конкретных исследованиях.
Управление факторами. Предположим, что в рассмотренном выше примере анализа двух выборок мы добавим еще один фактор, например, Пол - Gender. Пусть каждая группа теперь состоит из 3 мужчин и 3 женщин. План этого эксперимента можно представить в виде таблицы 2 на 2:
| Экспериментальная группа 1 |
Экспериментальная группа 2 |
|
|---|---|---|
| Мужчины |
2 3 1 |
6 7 5 |
| Среднее | 2 | 6 |
| Женщины |
4 5 3 |
8 9 7 |
| Среднее | 4 | 8 |
До проведения вычислений можно заметить, что в этом примере общая дисперсия имеет, по крайней мере, три источника: (1) случайная ошибка (внутригрупповая дисперсия), (2) изменчивость, связанная с принадлежностью к экспериментальной группе, и (3) изменчивость, обусловленная полом объектов наблюдения. (Отметим, что существует еще один возможный источник изменчивости - взаимодействие факторов, который мы обсудим позднее). Что произойдет, если мы не будем включать пол как фактор при проведении анализа и вычислим обычный t-критерий? Если мы будем вычислять суммы квадратов, игнорируя пол (т.е. объединяя объекты разного пола в одну группу при вычислении внутригрупповой дисперсии и получив при этом сумму квадратов для каждой группы равную SS =10 и общую сумму квадратов SS = 10+10 = 20), то получим большее значение внутригрупповая дисперсии, чем при более точном анализе с дополнительным разбиением на подгруппы по полу (при этом внутригрупповые средние будут равны 2, а общая внутригрупповая сумма квадратов равна SS = 2+2+2+2 = 8).
Итак, при введении дополнительного фактора: пол, остаточная дисперсия уменьшилась. Это связано с тем, что среднее значение для мужчин меньше, чем среднее значение для женщин, и это различие в средних значениях увеличивает суммарную внутригрупповую изменчивость, если фактор пола не учитывается. Управление дисперсией ошибки увеличивает чувствительность (мощность) критерия. На этом примере видно еще одно преимущество дисперсионного анализа по сравнению с обычным t-критерием для двух выборок. Дисперсионный анализ позволяет изучать каждый фактор, управляя значениями других факторов. Это, в действительности, и является основной причиной его большей статистической мощности (для получения значимых результатов требуются меньшие объемы выборок). По этой причине дисперсионный анализ даже на небольших выборках дает статистически более значимые результаты, чем простой t-критерий.
Существует еще одно преимущество дисперсионного анализа перед обычным t-критерием: дисперсионный анализ позволяет обнаружить эффекты взаимодействия между факторами и, поэтому, позволяет проверять более сложные гипотезы. Рассмотрим еще один пример, иллюстрирующий только что сказанное. (Термин взаимодействие впервые был использован Фишером в работе Fisher, 1926)
Главные эффекты, попарные (двухфакторные) взаимодействия. Предположим, что имеется две группы студентов, причем психологически студенты первой группы настроены на выполнение поставленных задач и более целеустремленны, чем студенты второй группы, состоящей из более ленивых студентов. Разобьем каждую группу случайным образом пополам и предложим одной половине в каждой группе сложное задание, а другой - легкое. После этого измерим, насколько напряженно студенты работают над этими заданиями. Средние значения для этого (вымышленного) исследования показаны в таблице:
| Целеустремленные | Ленивые | |
|---|---|---|
| Трудное задание Легкое задание |
10 5 |
5 10 |
Какой вывод можно сделать из этих результатов? Можно ли заключить, что: (1) над сложным заданием студенты трудятся более напряженно; (2) честолюбивые студенты работают упорнее, чем ленивые? Ни одно из этих утверждений не отражает сущность систематического характера средних, приведенных в таблице. Анализируя результаты, правильнее было бы сказать, что над сложными заданиями работают упорнее только честолюбивые студенты, в то время как над легкими заданиями только ленивые работают упорнее. Другими словами характер студентов и сложность задания взаимодействуя между собой влияют на затрачиваемое усилие. Это является примером попарного взаимодействия между характером студентов и сложностью задания. Заметим, что утверждения 1 и 2 описывают главные эффекты.
Взаимодействия высших порядков. В то время как объяснить попарные взаимодействия еще сравнительно легко, взаимодействия высших порядков объяснить значительно сложнее. Представьте, что в рассматриваемый выше пример, введен еще один фактор пол и получена следующая таблица средних значений:
| Женщины | Целеустремленные | Ленивые |
|---|---|---|
| Трудное задание Легкое задание |
10 5 |
5 10 |
| Мужчины | Целеустремленные | Ленивые |
| Трудное задание Легкое задание |
1 6 |
6 1 |
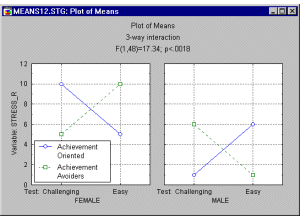
Какие теперь выводы можно сделать из полученных результатов? Графики средних позволяют объяснять сложные эффекты. Модуль дисперсионного анализа позволяет строить эти графики практически одним щелчком мыши. Изображение на этих графике внизу представляет собой изучаемое трехфакторное взаимодействие.

Глядя на график, можно сказать, что у женщин существует взаимодействие между характером и сложностью теста: целеустремленные женщины работают над трудным заданием более напряженно, чем над легким. У мужчин то же взаимодействие носит обратный характер. Видно, что описание взаимодействия между факторами становится более запутанным.
Общий способ описания взаимодействий. В общем случае взаимодействие между факторами описывается в виде изменения одного эффекта под воздействием другого. В рассмотренном выше примере двухфакторное взаимодействие можно описать как изменение главного эффекта фактора, характеризующего сложность задачи, под воздействием фактора, описывающего характер студента. Для взаимодействия трех факторов из предыдущего параграфа можно сказать, что взаимодействие двух факторов (сложности задачи и характера студента) изменяется под воздействием Пола. Если изучается взаимодействие четырех факторов, можно сказать, что взаимодействие трех факторов, изменяется под воздействием четвертого фактора, т.е. существуют различные типы взаимодействий на разных уровнях четвертого фактора. Оказалось, что во многих областях взаимодействие пяти или даже большего количества факторов не является чем-то необычным.
| В начало |
В этом разделе будет дан обзор основных "кирпичиков", из которых строятся сложные планы.
Для просмотра других разделов Вводного обзора выберите соответствующее название ниже.
См. также Методы дисперсионного анализа, Компоненты дисперсии и смешанные модели ANOVA/ANCOVA и Планирование экспермента.
Межгрупповые планы и планы с повторными измерениями
При сравнении двух различных групп обычно используется t-критерий для независимых выборок (из модуля Основные статистики и таблицы). Когда сравниваются две переменные на одном и том же множестве объектов (наблюдений), используется t-критерий для зависимых выборок. Для дисперсионного анализа также важно зависимы или нет выборки. Если имеются повторные измерения одних и тех же переменных (при разных условиях или в разное время) для одних и тех же объектов, то говорят о наличии фактора повторных измерений (называемого также внутригрупповым фактором, поскольку для оценки его значимости вычисляется внутригрупповая сумма квадратов). Если сравниваются разные группы объектов (например, мужчины и женщины, три штамма бактерий и т.п.), то разница между группами описывается межгрупповым фактором. Способы вычисления критериев значимости для двух описанных типов факторов различны, но общая их логика и интерпретации совпадает.
Меж- и внутригрупповые планы. Во многих случаях эксперимент требует включение в план и межгруппового фактора, и фактора повторных измерений. Например, измеряются математические навыки студентов женского и мужского пола (где пол -межгрупповой фактор) в начале и в конце семестра. Два измерения навыков каждого студента образуют внутригрупповой фактор (или фактор с повторными измерениями). Интерпретация главных эффектов и взаимодействий для межгрупповых факторов и факторов повторных измерений совпадает, и оба типа факторов могут, очевидно, взаимодействовать между собой (например, женщины приобретают навыки в течение семестра, а мужчины их теряют).
Во многих случаях можно пренебречь эффектом взаимодействия. Это происходит или когда известно, что в популяции эффект взаимодействия отсутствует, или когда осуществление полного факторного плана невозможно. Например, пусть изучается влияние четырех добавок к топливу на расход горючего. Выбираются четыре автомобиля и четыре водителя. Полный факторный эксперимент требует, чтобы каждая комбинация: добавка, водитель, автомобиль - появились хотя бы один раз. Для этого нужно не менее 4 x 4 x 4 = 64 групп испытаний, что требует слишком больших временных затрат. Кроме того, вряд ли существует взаимодействие между водителем и добавкой к топливу. Принимая это во внимание, можно использовать план типа Латинские квадраты, в котором содержится лишь 16 групп испытаний (четыре добавки обозначаются буквами A, B, C и D):
| Автомобиль | ||||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Водитель 1 Водитель 2 Водитель 3 Водитель 4 |
A B C D |
B C D A |
C D A B |
D A B C |
Латинские квадраты описаны в большинстве книг по планированию экспериментов (например, Hays, 1988; Lindman, 1974; Milliken and Johnson, 1984; Winer, 1962), и здесь они не будут детально обсуждаться. Отметим, что латинские квадраты это неnолные планы, в которых участвуют не все комбинации уровней факторов. Например, водитель 1 управляет автомобилем 1 только с добавкой А, водитель 3 управляет автомобилем 1 только с добавкой С. Уровни фактора добавки (A, B, C и D) вложены в ячейки таблицы автомобиль x водитель как яйца в гнезда. Это мнемоническое правило полезно для понимания природы гнездовых планов. Модуль Дисперсионный анализ предоставляет простые способы анализ планов такого типа.
Отметим, что анализ планов такого типа возможен и в некоторых других модулях системы STATISTICA. Подробнее см. в разделе Методы дисперсионного анализа. В частности, модуль Компоненты дисперсии и смешанные модели ANOVA/ANCOVA очень эффективен при анализе планов с несбалансированной вложенностью (т.е. когда вложенные факторы имеют различное число уровней при разных уровнях факторов, в которые они вложены), очень больших гнездовых планов (например, с общим числом уровней более 200) или иерархически вложенных планов (содержащих или не содержащих случайные факторы).
| В начало |
Ковариационный анализ (ANCOVA)
Основная идея
В разделе Основные идеи кратко обсуждалась идея управления факторами и то, каким образом включение аддитивных факторов позволяет уменьшить остаточную сумму квадратов и увеличить статистическую мощность плана. Все это может быть распространено и на переменные с непрерывным множеством значений. Когда такие непрерывные переменные включаются в план в качестве факторов, они называются ковариатами.
Для просмотра других разделов Вводного обзора выберите соответствующее название ниже.
См. также Методы дисперсионного анализа, Компоненты дисперсии и смешанные модели ANOVA/ANCOVA и Планирование эксперимента.
Предположим, что сравниваются математические навыки двух групп студентов, которые обучались по двум различным учебникам. Предположим также, что имеются дополнительные данные о коэффициенте интеллекта (IQ) каждого студента. Можно предположить, что коэффициент интеллекта связан с математическими навыками, и использовать эту информацию. Для каждой из двух групп студентов можно вычислить коэффициент корреляции между IQ и математическими навыками (см. Основные статистики и таблицы). Используя этот коэффициент корреляции, можно выделить долю дисперсии в группах, объясняемую IQ и необъясняемую долю дисперсии (см. также Элементарные понятия статистики и Основные статистики и таблицы). Оставшаяся доля дисперсии используется при проведении анализа как дисперсия ошибки. Если имеется корреляция между IQ и математическими навыками, то таким образом можно существенно уменьшить дисперсию ошибки SS/(n-1).
Влияние ковариат на F критерий. F критерий оценивает статистическую значимость различия средних в группах, при этом вычисляется отношение межгрупповой дисперсии (MSошибка) к дисперсии ошибок (MSошибка). Если MSошибка уменьшается, например, при учете фактора IQ, значение F увеличивается.
Множество ковариат. Рассуждения, использованные выше для одной ковариаты (IQ), легко распространяются на несколько ковариат. Например, кроме IQ, можно включить измерение мотивации, пространственного мышления и т.д. Вместо обычного коэффициента корреляции при этом используется множественный коэффициент корреляции (см. раздел Множественная регрессия).
Когда значение F-критерия уменьшается. Иногда введение ковариат в план эксперимента уменьшает значение F-критерия. Обычно это указывает на то, что ковариаты коррелированы не только с зависимой переменной (например, математическими навыками), но и с факторами (например, с разными учебниками). Предположим, что IQ измеряется в конце семестра, после почти годового обучения двух групп студентов по двум разным учебникам. Хотя студенты разбивались на группы случайным образом, может оказаться, что различие учебников настолько велико, что и IQ и математические навыки в разных группах будут сильно различаться. В этом случае, ковариаты не только уменьшают дисперсию ошибок, но и межгрупповую дисперсию. Другими словами, после контроля за разностью IQ в разных группах, разность в математических навыках уже будет несущественной. Ту же мысль можно выразить иначе: после "исключения" влияния IQ, неумышленно исключается и влияние учебника на развитие математических навыков.
Скорректированные средние. Когда ковариата влияет на межгрупповой фактор, следует вычислять скорректированные средние, т.е. такие средние, которые получаются после удаления всех оценок ковариат.
Взаимодействие между ковариатами и факторами. Также как исследуется взаимодействие между факторами, можно исследовать взаимодействия между ковариатами и группами факторов. Предположим, что один из учебников особенно подходит для умных студентов. Второй учебник для умных студентов скушен, а для менее умных студентов этот же учебник труден. В результате имеется положительная корреляция между IQ и результатом обучения в первой группе (более умные студенты, лучше результат) и нулевая или небольшая отрицательная корреляция во второй группе (чем умнее студент, тем менее вероятно приобретение математических навыков из второго учебника). В некоторых исследованиях эта ситуация обсуждается как пример нарушения предположений ковариационного анализа (см. Предположения и последствия их нарушения). Однако так как в модуле Дисперсионный анализ используются самые общие способы ковариационного анализа, можно, в частности, оценить статистическую значимость взаимодействия между факторами и ковариатами.
В то время как фиксированные ковариаты обсуждаются в учебниках достаточно часто, переменные ковариаты упоминаются намного реже. Обычно, при проведении экспериментов с повторными измерениями, нас интересуют различия в измерениях одних и тех же величин в разные моменты времени. А именно, нас интересует значимость этих различий. Если одновременно с измерениями зависимых переменных проводится измерение ковариат, можно вычислить корреляцию между ковариатой и зависимой переменной. Например, можно изучать интерес к математике и математические навыки в начале и в конце семестра. Интересно было бы проверить, коррелированы ли между собой изменения в интересе к математике с изменением математических навыков. Модуль Дисперсионный анализ в STATISTICA автоматически оценивает статистическую значимость изменения ковариат в тех планах, где это возможно.
| В начало |
Многомерные планы: Многомерный дисперсионный и ковариационный анализ
Для просмотра других обзорных разделов выберите соответствующее название ниже.
См. также Методы дисперсионного анализа, Компоненты дисперсии и смешанные модели ANOVA/ANCOVA и Планирование эксперимента.
Все рассматриваемые ранее примеры включали только одну зависимую переменную. Когда одновременно имеется несколько зависимых переменных, возрастает лишь сложность вычислений, а содержание и основные принципы не меняются. Например, проводится исследование двух различных учебников. При этом изучаются успехи студентов в изучении физики и математики. В этом случае имеются две зависимые переменные и нужно выяснить, как влияют на них одновременно два разных учебника. Для этого можно воспользоваться многомерным дисперсионным анализом (MANOVA). Вместо одномерного F критерия, используется многомерный F критерий (лямбда-критерий Уилкса), основанный на сравнении ковариационной матрицы ошибок и межгрупповой ковариационной матрицы. Если зависимые переменные коррелированы между собой, то эта корреляция должна учитываться при вычислении критерия значимости. Очевидно, если одно и то же измерение повторяется дважды, то ничего нового получить при этом нельзя. Если к имеющемуся измерению добавляется коррелированное с ним измерение, то получается некоторая новая информация, но при этом новая переменная содержит избыточную информацию, которая отражается в ковариации между переменными.
Интерпретация результатов. Если общий многомерный критерий значим, можно заключить, что соответствующий эффект (например, тип учебника) значим. Однако встают следующие вопросы. Влияет ли тип учебника на улучшение только математических навыков, только физических навыков, или одновременно на улучшение тех и других навыков. В действительности, после получения значимого многомерного критерия, для отдельного главного эффекта или взаимодействия исследуются одномерные F-критерии. Другими словами, отдельно исследуются зависимые переменные, которые вносят вклад в значимость многомерного критерия.
Планы с повторными измерениями
Если измеряются математические и физические навыки студентов в начале семестра и в конце семестра, то это и есть повторные измерения. Изучение критерия значимости в таких планах это логическое развитие одномерного случая. Заметим, что методы многомерного дисперсионного анализа обычно также используются для исследования значимости одномерных факторов повторных измерений, имеющих более чем два уровня. Соответствующие применения будут рассмотрены позднее в этой части.
Суммы значений переменной и дисперсионный анализ
Даже опытные пользователи одномерного и многомерного дисперсионного анализа часто приходят в затруднение, получая разные результаты при применении многомерного дисперсионного анализа, например, для трех переменных, и при применении одномерного дисперсионного анализа к сумме этих трех переменных, как к одной переменной. Идея суммирования переменных состоит в том, что каждая переменная содержит в себе некоторую истинную переменную, которая и исследуется, а также случайную ошибку измерения. Поэтому при усреднении значений переменных, ошибка измерения будет ближе к 0 для всех измерений и усредненное значений будет более надежным. На самом деле, в этом случае применение дисперсионного анализа к сумме переменных разумно и является мощным методом. Однако, если зависимые переменные по своей природе многомерны, то суммирование неуместно. Например, пусть зависимые переменные состоят из четырех показателей успеха в обществе. Каждый показатель характеризует совершенно независимую сторону человеческой деятельности (например, профессиональный успех, преуспевание в бизнесе, семейное благополучие и т.д.). Сложение этих переменных подобно сложению яблока и апельсина. Сумма этих переменных не будет подходящим одномерным показателем. Поэтому с такими данными нужно обходится как с многомерными показателями в многомерном дисперсионном анализе.
| В начало |
Анализ контрастов и апостериорные критерии
Для просмотра других обзорных разделов выберите соответствующее название ниже.
См. также Методы дисперсионного анализа, Компоненты дисперсии и смешанные модели ANOVA/ANCOVA и Планирование эксперимента.
Почему сравниваются отдельные множества средних?
Обычно гипотезы относительно экспериментальных данных формулируются не просто в терминах главных эффектов или взаимодействий. Примером может служить такая гипотеза: некоторый учебник повышает математические навыки только у студентов мужского пола, в то время как другой учебник примерно одинаково эффективен для обоих полов, но все же менее эффективен для мужчин. Можно предсказать, что эффективность учебника взаимодействует с полом студента. Однако этот прогноз касается также природы взаимодействия. Ожидается значительное различие между полами, обучающимися по одной книге, и практически не зависимые от пола результаты для обучающихся по другой книге. Такой тип гипотез обычно исследуется с помощью анализа контрастов.
Если говорить коротко, то анализ контрастов позволяет оценивать статистическую значимость некоторых линейных комбинаций факторов сложного плана. Анализ контрастов главный и обязательный элемент любого сложного плана дисперсионного анализа. Модуль Дисперсионный анализ имеет достаточно разнообразные возможности анализа контрастов, которые позволяют выделять и анализировать любые типы сравнений средних (способы задания контрастов описаны в разделе Примечания).
Апостериорные критерииИногда в результате обработки эксперимента обнаруживаются неожиданные различия в средних. Хотя в большинстве случаев творческий исследователь сможет объяснить эти различия, ему сложно провести дальнейший анализ. Эта проблема является одной из тех, для которых используются апостериорные критерии, то есть критерии, не использующие априорные гипотезы. Для иллюстрации рассмотрим следующий эксперимент. Предположим, что на 100 карточках записаны числа от 1 до 10. Опустив все эти карточки в шапку, мы случайным образом выбираем 20 раз по 5 карточек, и вычисляем для каждой выборки среднее значение (среднее чисел, записанных на карточки). Можно ли ожидать, что найдется две выборки, у которых средние значения значимо отличаются? Это очень правдоподобно! Выбирая две выборки с максимальным и минимальным средним, можно получить разность средних значений, сильно отличающуюся от разности средних значений, например, первых двух выборок. Эту разность можно исследовать, например, с помощью анализа контрастов. Если не вдаваться в детали, то существует несколько, так называемых апостериорных критериев, которые основаны в точности на первом сценарии (взятие экстремальных средних из 20 выборок), т. е. эти критерии основаны на выборе наиболее отличающихся средних для сравнения всех средних значений в плане. Модуль Дисперсионный анализ предлагает широкий выбор таких критериев. Когда в эксперименте встречаются неожиданные результаты, то используются апостериорные процедуры для исследования их статистической значимости.
| В начало |
Предположения и последствия их нарушения
Для просмотра других обзорных разделов выберите соответствующее название ниже.
См. также Методы дисперсионного анализа, Компоненты дисперсии и смешанные модели ANOVA/ANCOVA и Планирование эксперимента.
Предположения. Имеются следующие предположения дисперсионного анализа: зависимая переменная измерена в интервальной шкале (см. раздел Элементарные понятия статистики); зависимая переменная имеет нормальное распределение внутри каждой группы. Модуль Дисперсионный анализ содержит широкий набор графиков и статистик для проверки этих предположений.
Эффекты нарушения. Вообще F-критерий очень устойчив к отклонению от нормальности (подробнее см. Lindman, 1974). Если эксцесс (см. Основные статистики и таблицы) больше 0, то значение статистики F может стать очень маленьким. Нулевая гипотеза при этом не может быть отвергнута, хотя она и не верна. Ситуация меняется на противоположную, если эксцесс меньше 0. Асимметрия распределения обычно незначительно влияет на F статистику. Если число наблюдений в ячейке достаточно большое, то отклонение от нормальности не имеет особого значения в силу центральной предельной теоремы, в соответствии с которой, распределение среднего значения при большом объеме выборки близко к нормальному, независимо от начального распределения. Подробное обсуждение устойчивости F статистики можно найти в Box and Anderson (1955) или Lindman (1974).
Предположения. Предполагается, что дисперсии в разных группах одинаковы. Это предположение называется предположением об однородности дисперсии. Напомним, что в предыдущих разделах описывая вычисление суммы квадратов ошибок мы производили суммирование внутри каждой группы. Если дисперсии в двух группах отличаются друг от друга, то сложение их не естественно и не дает верной оценки общей внутригрупповой дисперсии (так как в этом случае общей дисперсии вообще не существует). Модуль Дисперсионный анализ -ANOVA/MANOVA содержит большой набор статистических критериев, позволяющих обнаружить неоднородность дисперсии.
Эффекты нарушения. Линдман (Lindman 1974, стр. 33) показывает, что F критерий вполне устойчив относительно нарушения предположений однородности дисперсии (см. также Box, 1954a, 1954b; Hsu, 1938).
Специальный случай: коррелированность средних и дисперсий. Бывают случаи, когда F статистика может вводить в заблуждение. Это бывает, когда в ячейках плана средние значения коррелированы с дисперсией. Модуль Дисперсионный анализ позволяет строить диаграммы рассеяния дисперсии или стандартного отклонения относительно средних для обнаружения такой корреляции. Причина, по которой такая корреляция опасна, состоит в следующем. Представим себе, что имеется 8 ячеек в плане, 7 из которых имеют почти одинаковое среднее, а в одной ячейке среднее намного больше остальных. Тогда F критерий может обнаружить статистически значимый эффект. Но предположим, что в ячейке с большим средним значением и дисперсия значительно больше остальных, т.е. среднее значение и дисперсия в ячейках зависимы (чем больше среднее, тем больше дисперсия). В этом случае большое среднее значение ненадежно, так как оно может быть вызвано большой дисперсией данных. Однако F статистика, основанная на объединенной дисперсии внутри ячеек, будет фиксировать большое среднее, хотя критерии, основанные на дисперсии в каждой ячейке не все различия в средних будут считать значимыми.
Такой характер данных (большое среднее и большая дисперсия) часто встречается, когда имеются резко выделяющиеся наблюдения. Одно или два резко выделяющихся наблюдений сильно смещают среднее значение и очень увеличивают дисперсию.
Однородность дисперсии и ковариаций
Предположения. В многомерных планах, с многомерными зависимыми измерениями, также применяются предположение об однородности дисперсии, описанные ранее. Однако так как существуют многомерные зависимые переменные, то требуется так же чтобы их взаимные корреляции (ковариации) были однородны по всем ячейкам плана. Модуль Дисперсионный анализ предлагает разные способы проверки этих предположений.
Эффекты нарушения. Многомерным аналогом F- критерия является лямбда-критерий Уилкса. Не так много известно об устойчивости (робастности) лямбда-критерия Уилкса относительно нарушения указанных выше предположений. Тем не менее, так как интерпретация результатов модуля Дисперсионный анализ основывается обычно на значимости одномерных эффектов (после установления значимости общего критерия), обсуждение робастности касается, в основном, одномерного дисперсионного анализа. Поэтому должна быть внимательно исследована значимость одномерных эффектов.
Специальный случай:ковариационный анализ. Особенно серьезные нарушения однородности дисперсии/ковариаций могут происходить, когда в план включаются ковариаты. В частности, если корреляция между ковариатами и зависимыми измерениями различна в разных ячейках плана, может последовать неверное истолкование результатов. Следует помнить, что в ковариационном анализе, в сущности, проводится регрессионный анализ внутри каждой ячейки для того, чтобы выделить ту часть дисперсии, которая соответствует ковариате. Предположение об однородности дисперсии/ковариации предполагает, что этот регрессионный анализ проводится при следующем ограничении: все регрессионные уравнения (наклоны) для всех ячеек одинаковы. Если это не выполняется, могут появиться большие ошибки. Модуль Дисперсионный анализ имеет несколько специальных критериев для проверки этого предположения. Можно посоветовать использовать эти критерии, для того, чтобы убедиться, что регрессионные уравнения для различных ячеек примерно одинаковы.
Сферичность и сложная симметрия
Причины использования многомерного подхода к повторным измерениям в дисперсионном анализе. В планах, содержащих факторы повторных измерений с более чем двумя уровнями, применение одномерного дисперсионного анализа требует дополнительных предположений: предположения о сложной симметрии и о сферичности. Эти предположения редко выполняются (см. ниже). Поэтому в последние годы многомерный дисперсионный анализ завоевал популярность в таких планах (оба подхода совмещены в модуле Дисперсионный анализ). Предположение о сложной симметрии состоит в том, что дисперсии (общие внутригрупповые) и ковариации (внутри групп) для различных повторных измерений однородны (одинаковы). Это достаточное условие для того, чтобы одномерный F критерий для повторных измерений был обоснованным (т.е. выданные F-значения в среднем соответствовали F-распределению). Однако, в данном случае, это не условие не является необходимым. Условие сферичности является необходимым и достаточным условием для обоснованного применения F-критерия. Смысл условия состоит в том, что внутри групп все наблюдения должны быть независимы и одинаково распределены. Природа этих предположений, а также влияние их нарушений обычно не очень хорошо описаны в книгах по дисперсионному анализу. Мы даем это описание в следующих параграфах. Там же будет показано, что результаты одномерного подхода могут отличаться от результатов многомерного подхода, и будет объяснено, что это означает.
Необходимость независимости гипотез. Общий способ анализа данных в дисперсионном анализе - это подгонка модели. Если относительно модели, соответствующей данным, имеются некоторые априорные гипотезы, то дисперсия разбивается для проверки этих гипотез (проверка главных эффектов, взаимодействий). С вычислительной точки зрения этот подход строит некоторое множество контрастов (множество сравнений средних в плане). Однако если контрасты не независимы друг от друга, то разбиение дисперсии на компоненты не имеет смысла. Например, если два контраста A и B тождественны, то соответственная им компонента дисперсии выделяется дважды. Например, глупо и бессмысленно выделять две гипотезы: "среднее в ячейке 1 выше среднего в ячейке 2" и "среднее в ячейке 1 выше среднего в ячейке 2". Итак, гипотезы должны быть независимы или ортогональны (термин ортогональность впервые использован в работе Yates, 1933).
Независимые гипотезы при повторных измерениях. Общий алгоритм, реализованный в модуле Дисперсионный анализ, будет пытаться для каждого эффекта генерировать независимые (ортогональные) контрасты (см. раздел Технические замечания руководства пользователя). Для фактора повторных измерений эти контрасты задают множество гипотез относительно разностей между уровнями рассматриваемого фактора. Однако если эти разности коррелированы внутри групп, то результирующие контрасты не являются больше независимыми. Например, в обучении, где обучающиеся измеряются три раза за один семестр, может случиться, что изменения между 1 и 2 измерением отрицательно коррелируют с изменением между 2 и 3 измерениями субъектов. Те, кто большую часть материала освоил между 1 и 2 измерениями, осваивают меньшую часть в течение того времени, которое прошло между 2 и 3 измерением. В действительности, для большинства случаев, где дисперсионный анализ используются при повторных измерениях, можно предположить, что изменения по уровням коррелированы по субъектам. Однако когда это происходит, предположение о сложной симметрии и сферичности не выполняются и независимые контрасты не могут быть вычислены.
Влияние нарушений и способы их исправления. Когда предположения о сложной симметрии или о сферичности не выполняются, дисперсионный анализ может выдать ошибочные результаты. До того, как были достаточно разработаны многомерные процедуры, было предложено несколько предположений для компенсации нарушений этих предположений. (См., например, работы Greenhouse & Geisser, 1959 и Huynh & Feldt, 1970). Эти методы до сих пор широко используются (поэтому они представлены в модуле Дисперсионный анализ).
Подход многомерного дисперсионного анализа к повторным измерениям. В целом проблемы сложной симметрии и сферичности относятся к тому факту, что множества контрастов, включенных в исследование эффектов факторов повторных измерений (с числом уровней больше двух) не независимы друг от друга. Однако им не обязательно быть независимыми, если используется многомерный критерий для одновременной проверки статистического значимости двух или более контрастов фактора повторных измерений. Это является причиной того, что методы многомерного дисперсионного анализа стали чаще использоваться для проверки значимости факторов одномерных повторных измерений с более чем 2 уровнями. Этот подход широко распространен, так как он, в общем случае, не требует предположения о сложной симметрии и предположения о сферичности.
Случаи, в которых подход многомерного дисперсионного анализа не может быть использован. Существуют примеры (планы), когда подход многомерного дисперсионного анализа не может быть применен. Обычно это случаи, когда имеется небольшое количество субъектов в плане и много уровней в факторе повторных измерений. Тогда для проведения многомерного анализа может быть слишком мало наблюдений. Например, если имеется 12 субъектов, p = 4 фактора повторных измерений, и каждый фактор имеет k = 3 уровней. Тогда взаимодействие 4-х факторов будет "расходовать" (k-1)p = 24 = 16 степеней свободы. Однако имеется лишь 12 субъектов, следовательно, в этом примере многомерный тест не может быть проведен. Модуль Дисперсионный анализ самостоятельно обнаружит эти наблюдения и вычислит только одномерные критерии.
Различия в одномерных и многомерных результатах. Если исследование включает большое количество повторных измерений, могут возникнуть случаи, когда одномерный подход дисперсионного анализа к повторным измерениям дает результаты, сильно отличающиеся от тех, которые были получены при многомерном подходе. Это означает, что разности между уровнями соответствующих повторных измерений коррелированы по субъектам. Иногда этот факт представляет некоторый самостоятельный интерес.
Методы дисперсионного анализа обсуждаются в нескольких разделах этого учебника. Хотя многие из доступных статистических методов описываются одновременно в нескольких главах, каждый из них наиболее удобен при работе в определенной области приложений.
Диспресионный анализ: Эта глава включает обзор полнофакторных планов, планов с повторными измерениями, планов многомерного дисперсионного и ковариационного анализа (MANOVA), планов с балансированной вложенностью (планы бывают не сбалансированными, т.е. имеющими различные размеры выборок n при некоторых испытаниях), а также описание оценивания спланированных и апостериорных сравнений и мн. др.
Компоненты дисперсии и смешанная модель ANCOVA: Эта глава включает обсуждение экспериментов со случайными эффектами (смешанная модель дисперсионного анализ), оценивание компонент дисперсии для случайных эффектов, планов с большими главными эффектами (например, с факторами, имеющими более 100 уровней) с/без случайных эффектов, а также в случае планов с большим числом факторов, когда необходимо оценить все взаимодействия.
Планирование эксперимента: Эта глава включает обсуждение стандартных экспериментальных планов, используемых в промышленных/производственных приложениях, включая 2**(k-p) и 3**(k-p) планы, центральные композиционные и нефакторные планы, планы для смесей, D- и A-оптимальные планы, а также планы для произвольных ограниченных областей значений экспериментальных данных.
Анализ повторяемости и воспроизводимости (в главе Анализ процессов): Этот раздел главы Анализ процессов включает обсуждение планов специального вида, используемых для оценивания надежности и точности измерительных устройств; Эти планы обычно включают два или три случайных фактора и набор специализированных статистик, позволяющих оценить качество измерительной системы (обычно в промышленных/производственных приложениях).
Таблицы группировки (в главе Основные статистики и таблицы): Эта глава включает обсуждение экспериментов, одного (многоуровневого) или нескольких (любых) факторов в случаях, когда не требуется проведение полного дисперсионного анализа.
| В начало |
![]()
(c) Copyright StatSoft, Inc., 1984-1998
STATISTICA является торговой маркой StatSoft, Inc.