Моделирование структурными уравнениями

Моделирование структурными уравнениями

Обзор основных понятий

Наметившийся в последнее время прогресс в области многомерного статистического анализа и анализа корреляционных структур, объединенный с новейшими вычислительными алгоритмами, послужил отправной точкой для создания новой, но уже получившей признание, техники Моделирования структурными уравнениями. Эта, по сути дела, всеобъемлющая и необычайно мощная техника многомерного анализа включает большое количество методов из различных областей статистики. Кратко можно сказать, что SEPATH представляет собой мощное развитие многих методов многомерного анализа, а именно множественная регрессия и факторный анализ получили здесь естественное развитие и объединение. Далее в этой главе мы будем предполагать, что читатель уже знаком с основными статистическими понятиями, которые описаны в разделе Элементарные понятия статистики, в том числе с понятием дисперсии, ковариации и корреляции. Если вам кажется, что ваших знаний не достаточно для дальнейшего чтения, мы рекомендуем просмотреть раздел Основные статистики и таблицы, чтобы восполнить эти пробелы. Хотя это и не является обязательным, нам было бы проще объяснить вам возможности структурного моделирования, если бы предварительно вы получили некоторое представление о методах факторного анализа.

Основные задачи, для решения которых используются структурные уравнения следующие:

Причинное моделирование или анализ путей, при проведении которого предполагается, что между переменными имеются причинные взаимосвязи. Возможна проверка гипотез и подгонка параметров причинной модели, описываемой линейными уравнениями. Причинные модели могут включать явные или латентные переменные, или и те и другие;
Подтверждающий факторный анализ, используемый как развитие обычного факторного анализа для проверки определенных гипотез о структуре факторных нагрузок и корреляций между факторами;
Факторный анализ второго порядка, являющийся модификацией факторного анализа, при проведении которого для получения факторов второго порядка анализируется корреляционная матрица общих факторов;
Регрессионные модели, являющиеся модификацией Многомерного линейного регрессионного анализа, в котором коэффициенты регрессии могут быть зафиксированы равными друг другу или каким-нибудь заданным значениям;
Моделирование ковариационной структуры, которое позволяет проверить гипотезу о том, что матрица ковариации имеет определенный вид. Например, с помощью этой процедуры вы можете проверить гипотезу о равенстве дисперсий у всех переменных;
Модели корреляционной структуры, которое позволяет проверить гипотезу о том, что матрица корреляции имеет определенный вид. Классическим примером является гипотеза о том, что матрица корреляции имеет циклическую структуру (см. книгу Guttman, 1954; Wiggins, Steiger, и Gaelick, 1981);
Модели структуры средних, которые позволяют исследовать структуру средних, например, одновременно с анализом дисперсий и ковариаций.

Многие виды моделей попадают сразу в несколько из этих категорий, поэтому при практическом анализе структурной модели не так-то просто ее классифицировать, да в этом и нет особой необходимости.

Структурные уравнения, включающие только линейные связи между явными и латентными переменными, могут быть изображены в виде диаграмм путей. Поэтому даже начинающий пользователь может провести сложный анализ с минимальными затратами времени на обучение.

В начало

Идеи, лежащие в основе структурного моделирования

Одной из основных используемых идей, с которой знакомятся все начинающие изучение статистики, является эффект воздействия аддитивных и мультипликативных преобразований. Как учат студентов, если умножить каждое число на некоторую константу K, среднее значение также умножиться на K. При этом стандартное отклонение умножится на модуль K.

Например, рассмотрим набор из трех чисел 1, 2, 3. Эти числа имеют среднее равное 2 и стандартное отклонение равное 1. Далее, пусть мы умножили все три числа на 4. Тогда среднее значение будет равно 8, стандартное отклонение примет значение 4, а дисперсия будет равна 16.

Таким образом, если мы имеем набор чисел X связанные с другим набором чисел Y зависимостью Y = 4X, то дисперсия Y должна быть в16 раз больше, чем дисперсия X. Поэтому мы можем проверить гипотезу о том, что Y и X связаны уравнением Y = 4X, косвенно - сравнением дисперсий переменных Y и X.

Эта идея может быть различными способами обобщена на несколько переменных, связанных системой линейных уравнений. При этом правила преобразований становятся более громоздкими, вычисления более сложными, но основной смысл остается прежним - вы можете проверить связаны ли переменные линейной зависимостью, изучая их дисперсии и ковариации.

Для проверки имеет ли ковариационная матрица заданную структуру статистики используют несколько процедур. Процесс структурного моделирования состоит из следующих этапов:

вы описываете (обычно с помощью диаграммы путей) модель, представляющую ваше понимание зависимостей между переменными;
программа определяет, с помощью специальных внутренних методов, какие значения дисперсий и ковариаций переменных получаются в текущей модели на основании входных данных;
программа проверяет, насколько хорошо полученные дисперсии и ковариации удовлетворяют нашей модели;
программа сообщает пользователю полученные результаты статистических испытаний, а также выводит оценки параметров и стандартные ошибки для численных коэффициентов в линейных уравнениях вмести с большим количеством дополнительной диагностической информации;
на основании этой информации, вы решаете, хорошо ли текущая модель согласуется с вашими данными.

Основные этапы процесса структурного моделирования описаны далее в тексте и показаны на диаграмме внизу. Во-первых, хотя логика математических вычислений при проведении структурного моделирования очень сложная, основные этапы соответствуют пяти шагам на диаграмме.

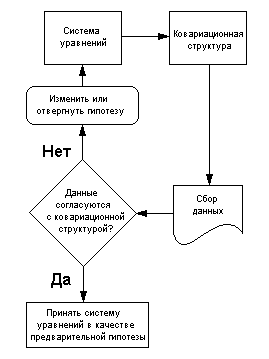
Во-вторых, следует помнить, что не разумно ожидать идеального соответствия модели и данных - по нескольким причинам. Структурные модели с линейными зависимостями являются только приближениями реальных явлений. Природные зависимости далеки от линейных. Поэтому, истинные зависимости между переменными, скорее всего, не линейны. Более того, истинность многих статистических предположений, накладываемых на проверяемую модель, остается под большим вопросом. На практике нас интересует не то "Идеально ли модель согласуется с данными?" а, "Согласуется ли она достаточно хорошо, чтобы быть полезной для практического использования и разумного объяснения структуры наблюдаемых данных?"
В-третьих, следует помнить, что идеальное соответствие модели данным не обязательно означает, что модель верна. Мы вообще не можем доказать, что модель верна - умение доказывать правильность модели эквивалентно умению предсказывать будующее. Например, вы можете сказать "Если Джо - кошка, то у Джо есть усы". Однако, из того, что "У Джо есть усы" не следует, что Джо - кошка. Аналогично, вы можете сказать, что "если определенная причинная модель верна, то она согласуется с наблюдаемыми данными". Однако, модель, согласующаяся с данными, не обязательно является верной. Возможно, существует другая модель, которая ничуть не хуже согласуется с теми же данными.

В начало

Моделирование структурными уравнениями и диаграммы путей

Диаграммы путей играют существенную роль в процессе структурного моделирования. Диаграммы путей напоминают используемые блок-схемы. Они изображают переменные, связанные линиями, которые используются для отображения причинных связей. Каждая связь или путь включает в себя две переменные (заключенные в прямоугольник или овал), соединенные стрелками (линиями, обычно прямыми, имеющими стрелку-указатель на одном конце) или дугами (линиями, обычно искривленными, без стрелок указателей).
Путевые диаграммы удобнее всего представлять в качестве инструмента для указания, какие переменные вызывают изменения в других переменных. Однако этого описание не является абсолютно точным. Можно дать более точное описание.

Рассмотрим классическое линейное регрессионное уравнение

Y = aX + e

И его представление в виде пути, показанное ниже.

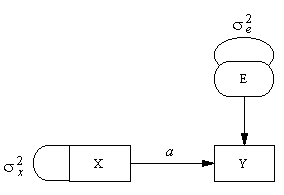
Такие диаграммы устанавливают простое взаимно-однозначное отображение, сохраняющее структуру модели, также называемое изоморфизмом. Все переменные в системе уравнений размещаются на диаграмме в прямоугольниках или овалах. Каждое уравнение отображается на диаграмме следующим путем: все независимые переменные (переменные в правой части уравнения) имеют стрелки, указывающие на независимые переменные. Весовые коэффициенты располагаются вблизи от соответствующих стрелок. Диаграмма снизу содержит представление системы простых линейных уравнений в виде диаграммы путей.

Отметим, что кроме представления линейных зависимостей в виде стрелок, диаграмма также содержит некоторые другие выражения. Во-первых, дисперсия независимых переменных, которая должна быть задана для проверки модели структурных связей, показаны на диаграмме с использованием изогнутых линий без стрелок. Такие линии мы называем дугами. Во-вторых, некоторые переменные, изображены в овальных, а не в прямоугольных рамках. Явные переменные (т.е., переменные, которые можно измерить непосредственно) на диаграммах изображаются внутри прямоугольников. Латентные переменные (т.е., которые нельзя непосредственно измерить, как, например, факторы в факторном анализе, или остатки в регрессионном) изображаются внутри овалов или окружностей. Например, переменная E на диаграмме сверху может рассматриваться как остаток линейной регрессии, когда значение Y предсказывается по значению X. Такие остатки не наблюдаются непосредственно, но в принципе могут быть вычислены по известным значениям Y и X (если a известно), поэтому они называются латентными (скрытыми) переменными и помещаются внутри овалов.

Мы рассмотрели очень простой пример диаграммы путей. В общем случае, мы заинтересованы в проверке намного более сложных моделей. Если же система уравнений становится слишком сложной, исследователи обычно переходят к рассмотрению ковариационных структур. В конце концов, модели становится настолько сложной и запутанной, что они перестают понимать ее основные принципы. Но есть доводы, которые говорят о том, что навыки проверки причинных моделей слабо связаны с проверкой линейных моделей. Переменные могут быть связаны нелинейно. Они могут быть линейно связаны по причинам, не относящимся к тому, что мы выбрали в качестве причины в нашей модели. Древнее изречение "наблюдаемая зависимость не означает причинной зависимости" остается верным, даже для сложной и многомерной корреляции. То, что причинное моделирование действительно позволяет исследовать, это насколько данные отличаются от соответствующих выводов причинной модели (а именно, от предполагаемой ковариационной структуры). Если система линейных уравнений, изоморфная диаграмме путей, хорошо согласуется с данными, это позволяет оставить модель для дальнейшего анализа или использования, но не доказывает ее истинность.

Хотя диаграммы путей могут использоваться для отражения причинных связей в наборе переменных, они не предполагают реального наличия таких связей. Диаграммы путей часто используются для простого и изоморфного представления системы линейных уравнений. По этому, они могут выражать линейные связи вне зависимости от того, имеются ли на самом деле описанные причинные связи. Следовательно, хотя мы интерпретируем диаграмму на рисунке сверху как "X влияет на Y", диаграмма также может обозначать графическое представление линейного регрессионного соотношения между X и Y.

В начало